Contents
2つの線分の長さの和が最小になるように点を定める

ヒロ
大学入試で良く出題される問題に,2つの線分の長さの和が最小になるように点の位置を定める問題がある。
2つの線分の和の最小値平面上に3点A,B,Cがあり,2つの線分AB,BCの長さの和が最小になるのは,3点A,B,Cが一直線上にあるときである。
2点が直線に関して反対側にあるとき

ヒロ
2点が直線に関して反対側にあるときは簡単であるが,言葉の意味を説明しておく。
2点が直線に関して反対側にある 平面上に1つの直線を引くことで,その平面は2つの領域に分けられる。2点が異なる領域にあるとき,「2点は直線に関して反対側にある」という。
例えば次の図では,点Pは直線 $l$ の上側の領域にあり,点Qは直線 $l$ の下側の領域にあるから,「2点P,Qは直線 $l$ に関して反対側にある」という。
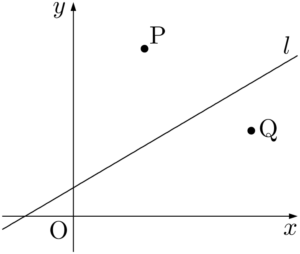
例えば次の図では,点Pは直線 $l$ の上側の領域にあり,点Qは直線 $l$ の下側の領域にあるから,「2点P,Qは直線 $l$ に関して反対側にある」という。


ヒロ
それでは次の問題を解説する。
2点を結ぶ最短経路の問題 次の図において,点Rを直線 $l$ 上の点とする。$\text{PR}+\text{RQ}$ を最小にする点Rの位置を求めて図示せよ。


【考え方と解答】
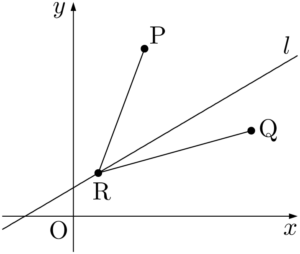
考えやすくするために,直線 $l$ 上の適当な位置に点Rをとると次のようになる。
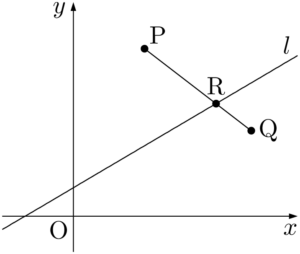
$\text{PR}+\text{RQ}$ が最小になるときは,折れ線PRQの長さが最小になるときである。2点P,Qを結ぶ最短経路は直線であるから,直線PQと直線 $l$ の交点をRにすれば,3点P,R,Qは一直線上にあるから,折れ線PRQの長さは最小になる。
考えやすくするために,直線 $l$ 上の適当な位置に点Rをとると次のようになる。

$\text{PR}+\text{RQ}$ が最小になるときは,折れ線PRQの長さが最小になるときである。2点P,Qを結ぶ最短経路は直線であるから,直線PQと直線 $l$ の交点をRにすれば,3点P,R,Qは一直線上にあるから,折れ線PRQの長さは最小になる。

2点が直線に関して同じ側にあるとき

ヒロ
次に,2点が直線に関して同じ側にあるときについて説明していく。
2点が直線に関して同じ側にある 平面上に1つの直線を引くことで,その平面は2つの領域に分けられる。2点が同じ領域にあるとき,「2点は直線に関して同じ側にある」という。
例えば次の図では,2点P,Qは直線 $l$ の上側の領域にあるから,「2点P,Qは直線 $l$ に関して同じ側にある」という。
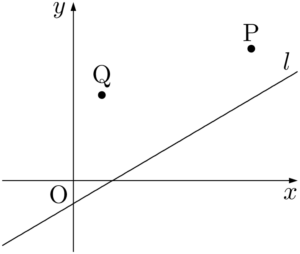
例えば次の図では,2点P,Qは直線 $l$ の上側の領域にあるから,「2点P,Qは直線 $l$ に関して同じ側にある」という。


ヒロ
それでは次の問題を解説する。
2点を結ぶ最短経路の問題2 次の図において,点Rを直線 $l$ 上の点とする。$\text{PR}+\text{RQ}$ を最小にする点Rの位置を求めて図示せよ。


【考え方と解答】
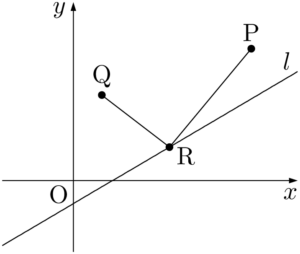
直線 $l$ 上の適当な位置に点Rをとると次のようになる。
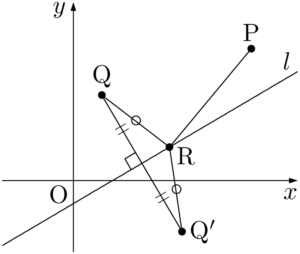
2点P,Qが直線 $l$ に関して反対側にある方が考えやすいから,いま考えている図で $\text{QR}=\text{Q}’\text{R}$ となるような点Q$’$を,2点Q,Q$’$ が直線 $l$ に関して反対側にあるようにとる。つまり,点Q$’$ は直線 $l$ に関して点Qと対称な点であり,図示すると次のようになる。
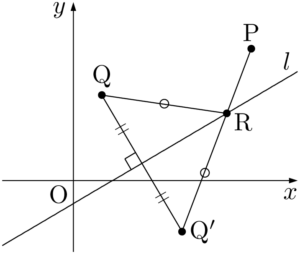
2点P,Qが直線 $l$ に関して反対側になるように,点Qを移した結果,折れ線PRQ$’$ の長さが最小になるような点Rの位置を考えることになる。これは結局,2点P,Q$’$ を結ぶ最短経路を考えて,直線PQ$’$ と直線 $l$ の交点をRとすれば折れ線PRQ$’$ の長さは最小になる。
今回は点Qを移して点Q$’$ をとったが,点Pの直線 $l$ に関して対称な点をとっても良い。
直線 $l$ 上の適当な位置に点Rをとると次のようになる。

2点P,Qが直線 $l$ に関して反対側にある方が考えやすいから,いま考えている図で $\text{QR}=\text{Q}’\text{R}$ となるような点Q$’$を,2点Q,Q$’$ が直線 $l$ に関して反対側にあるようにとる。つまり,点Q$’$ は直線 $l$ に関して点Qと対称な点であり,図示すると次のようになる。

2点P,Qが直線 $l$ に関して反対側になるように,点Qを移した結果,折れ線PRQ$’$ の長さが最小になるような点Rの位置を考えることになる。これは結局,2点P,Q$’$ を結ぶ最短経路を考えて,直線PQ$’$ と直線 $l$ の交点をRとすれば折れ線PRQ$’$ の長さは最小になる。

今回は点Qを移して点Q$’$ をとったが,点Pの直線 $l$ に関して対称な点をとっても良い。

ヒロ
考え方を理解することで忘れにくくなり,結局は「直線に関して対称な点」を求められるかどうかが重要ということである。


















