Contents
2点が直線に関してどのような位置関係にあるかチェックする方法

ヒロ
2点が直線に関して反対側にあるのか,同じ側にあるのかを確認したいときに,わざわざ図を描くのは面倒だと感じる人は多いだろう。

ヒロ
図を描けばすぐに確認できるが,図を描かずに確認したいときもあるだろう。

ヒロ
そんな場合に2点の位置関係を確認する方法を説明しておく。
【2点の位置関係を確認する方法】
直線 $l$ の方程式が $y=f(x)$ で表されているとし,2点A,Bの座標がA$(a,~b)$,B$(c,~d)$であるとする。点Aの座標について,$f(a)$ と $b$ の大小関係を調べる。仮に $b>f(a)$ となったとする。次に点Bの座標について,$f(c)$ と $d$ の大小関係を調べて,$d>f(c)$ となれば2点A,Bは直線 $l$ に関して同じ側にある。分かりにくいとは思うが,成り立つ不等号が同じ向きであれば,2点は直線に関して同じ側にあるし,不等号の向きが逆であれば,2点は直線に関して反対側にある。
直線 $l$ の方程式が $ax+by+c=0$ と一般形で与えられている場合もほとんど同じである。2点A,Bの座標を左辺の $ax+by+c$ に代入すると正か負のどちらかになるから,符号が等しければ同じ側,符号が異なれば反対側だと判断すればよい。
距離が最小になるように点を定める問題【国士舘大】
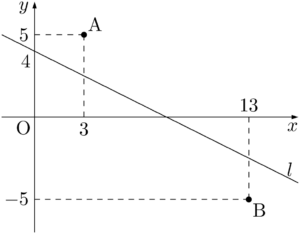
2015年 国士舘大 座標平面において,点A$(3,~5)$ とし,点Pを直線 $y=-\dfrac{1}{2}x+4$ 上の点とする。次の問に答えよ。
(1) 点B$(13,~-5)$ とするとき,$\text{AP}+\text{PB}$ を最小にする点Pの座標はP$\left(\myBox{ア},~\myBox{イ}\right)$ である。また,このとき,$\text{AP}+\text{PB}=\myBox{ウエ}\sqrt{\myBox{オ}}$ である。
(2) 点Qを直線 $y=-3x+34$ 上の点とする。点Pと点Qをともに動かすとき,$\text{AP}+\text{PQ}$ を最小にする点Pと点Qの座標は,それぞれP$\left(\myBox{カ},~\myBox{キ}\right)$,Q$\left(\myBox{クケ},~\myBox{コ}\right)$ である。
また,このとき $\text{AP}+\text{PQ}=\myBox{サ}\sqrt{\myBox{シス}}$ である。
(1) 点B$(13,~-5)$ とするとき,$\text{AP}+\text{PB}$ を最小にする点Pの座標はP$\left(\myBox{ア},~\myBox{イ}\right)$ である。また,このとき,$\text{AP}+\text{PB}=\myBox{ウエ}\sqrt{\myBox{オ}}$ である。
(2) 点Qを直線 $y=-3x+34$ 上の点とする。点Pと点Qをともに動かすとき,$\text{AP}+\text{PQ}$ を最小にする点Pと点Qの座標は,それぞれP$\left(\myBox{カ},~\myBox{キ}\right)$,Q$\left(\myBox{クケ},~\myBox{コ}\right)$ である。
また,このとき $\text{AP}+\text{PQ}=\myBox{サ}\sqrt{\myBox{シス}}$ である。
【(1)の考え方と解答】
直線 $y=-\dfrac{1}{2}x+4~\cdots\cdots①$ を $l$ とする。2点A,Bが $l$ に関して同じ側にあるのか,反対側にあるのかを確認する。点Aの座標に対して
個人的には,この結果に少し違和感を抱いた。通常の入試問題なら,2点A,Bが直線 $l$ に関して同じ側にあり,対称点をとって考えることが多い。しかし,この問題は2点A,Bが直線 $l$ に関して反対側にある。これだと簡単に解けてしまう。
実際,$\text{AP}+\text{PB}$ を最小にする $l$ 上の点Pは,直線ABと直線 $l$ の交点である。直線ABの傾きは
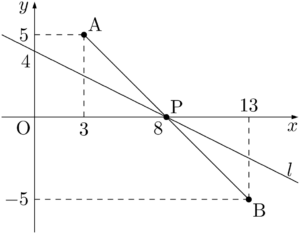
よって,求める点Pの座標はP$(8,~0)$ である。
このとき,$\text{AP}+\text{PB}=\text{AB}$ であるから
直線 $y=-\dfrac{1}{2}x+4~\cdots\cdots①$ を $l$ とする。2点A,Bが $l$ に関して同じ側にあるのか,反対側にあるのかを確認する。点Aの座標に対して
\begin{align*}
5>-\dfrac{1}{2}\Cdota3+4
\end{align*}
となる。また,点Bの座標に対して5>-\dfrac{1}{2}\Cdota3+4
\end{align*}
\begin{align*}
-5<-\dfrac{1}{2}\Cdota13+4
\end{align*}
となるから,2点A,Bは直線 $l$ に関して反対側にある。図を描けば次のように,2点A,Bが $l$ に関して反対側にあることが確認できる。-5<-\dfrac{1}{2}\Cdota13+4
\end{align*}

個人的には,この結果に少し違和感を抱いた。通常の入試問題なら,2点A,Bが直線 $l$ に関して同じ側にあり,対称点をとって考えることが多い。しかし,この問題は2点A,Bが直線 $l$ に関して反対側にある。これだと簡単に解けてしまう。
実際,$\text{AP}+\text{PB}$ を最小にする $l$ 上の点Pは,直線ABと直線 $l$ の交点である。直線ABの傾きは
\begin{align*}
\dfrac{-5-5}{13-3}=-1
\end{align*}
であるから,直線ABの方程式は\dfrac{-5-5}{13-3}=-1
\end{align*}
\begin{align*}
&y=-(x-3)+5 \\[4pt]&y=-x+8~\cdots\cdots②
\end{align*}
②を①に代入すると&y=-(x-3)+5 \\[4pt]&y=-x+8~\cdots\cdots②
\end{align*}
\begin{align*}
&-x+8=-\dfrac{1}{2}x+4 \\[4pt]&x=8
\end{align*}
このとき,②より $y=0$&-x+8=-\dfrac{1}{2}x+4 \\[4pt]&x=8
\end{align*}

よって,求める点Pの座標はP$(8,~0)$ である。
このとき,$\text{AP}+\text{PB}=\text{AB}$ であるから
\begin{align*}
\text{AB}&=\sqrt{(13-3)^2+(-5-5)^2} \\[4pt]&=\sqrt{10^2+10^2}=10\sqrt{2}
\end{align*}
\text{AB}&=\sqrt{(13-3)^2+(-5-5)^2} \\[4pt]&=\sqrt{10^2+10^2}=10\sqrt{2}
\end{align*}
(2) 点Qを直線 $y=-3x+34$ 上の点とする。点Pと点Qをともに動かすとき,$\text{AP}+\text{PQ}$ を最小にする点Pと点Qの座標は,それぞれP$\left(\myBox{カ},~\myBox{キ}\right)$,Q$\left(\myBox{クケ},~\myBox{コ}\right)$ である。
また,このとき $\text{AP}+\text{PQ}=\myBox{サ}\sqrt{\myBox{シス}}$ である。
【(2)の考え方と解答】
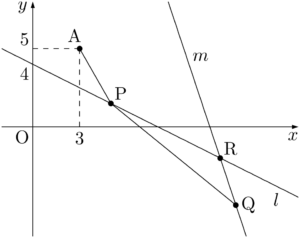
PとQの2点を動かす問題であるが,落ち着いて考えよう。直線 $y=-3x+34$ を $m$ とする。とりあえず深く考えずに $l$ 上に点P,$m$ 上に点Qをとると次のようになる。

上図の状態だと,2点A,Qが直線 $l$ に関して同じ側にあるから,面倒だなと感じるだろう。2直線 $l,~m$ の交点をRとして,点Qが点Rより右側になるようにすると,2点A,Qが直線 $l$ に関して反対側にある状態になる。
ここでふと(1)が頭によぎる。「もし(1)の点Bが直線 $m$ 上にあったら楽なのになぁ・・・」と思うことだろう。そして(1)で抱いた違和感や(1)の問題が簡単だった理由も,ここにあるのではないだろうかなどと考えてしまう。ということで点Bが直線 $m$ 上にあるかどうかをチェックしてみよう。点Bの $x$ 座標が13であり,$m:y=-3x+34$ に $x=13$ を代入すると
(1)の結果より,この場合に $\text{AP}+\text{PQ}$ が最小になるのは,点Qが点B$(13,~-5)$ に一致するときである。このときの点Pの座標は $(4,~2)$ であり,$\text{AP}+\text{PQ}$ の最小値は $10\sqrt{2}$ である。
しかし「これは(2)の解ではないだろう」と思うはず。これが解なら簡単すぎるということになるし,今回の問題は空欄を埋めるタイプで,そもそも空欄に当てはまらないから解でないことが確定する。ということで,点Aを $l$ に関して対称移動させて考える。
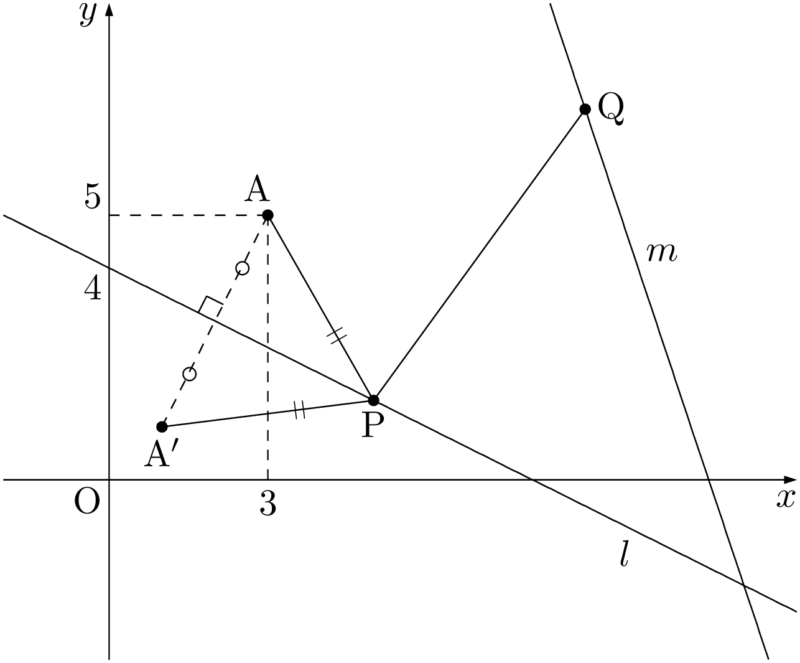
$l$ に関して点Aと対称な点A$’$ を考えることで,
ゴールまでの道筋も見えたから,点A$’$ の座標を求めて解答を前進させよう。
点A$’$ の座標を $(X,~Y)$ とおくとAA$’$の中点が直線 $l$ 上にあるから
よって,A$'(1,~1)$
次に,点A$’$ を通り,直線 $m$ に垂直な直線 $n$ の方程式を求める。$m$ の傾きは $-3$ であるから,$n$ の方程式は
よって,P$(4,~2)$ である。
また,点Qは2直線 $m,~n$ の交点であるから
よって,Q$(10,~4)$ である。
したがって,$\text{AP}+\text{PQ}$ の最小値は
点A$’$ と直線 $m:3x+y-34=0$ との距離を $d$ とすると
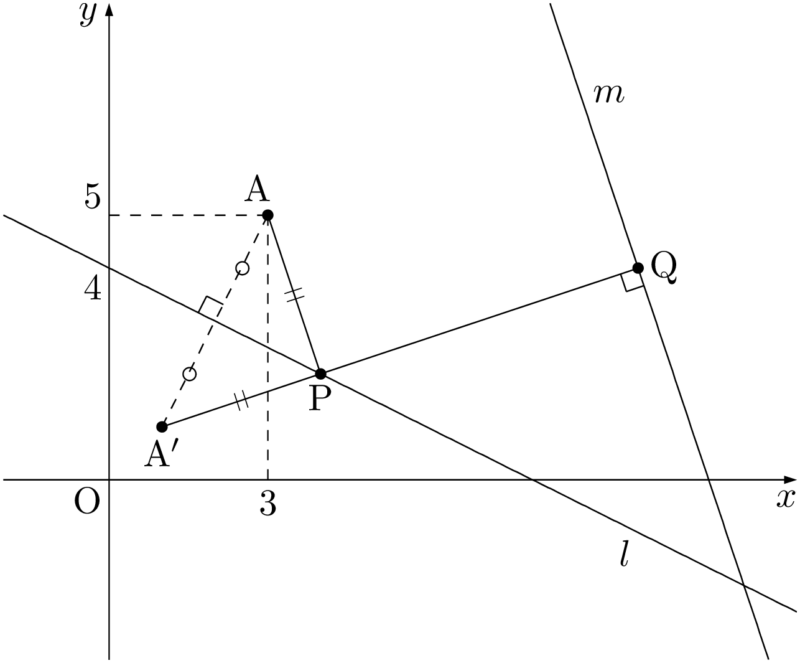

上図の状態だと,2点A,Qが直線 $l$ に関して同じ側にあるから,面倒だなと感じるだろう。2直線 $l,~m$ の交点をRとして,点Qが点Rより右側になるようにすると,2点A,Qが直線 $l$ に関して反対側にある状態になる。

ここでふと(1)が頭によぎる。「もし(1)の点Bが直線 $m$ 上にあったら楽なのになぁ・・・」と思うことだろう。そして(1)で抱いた違和感や(1)の問題が簡単だった理由も,ここにあるのではないだろうかなどと考えてしまう。ということで点Bが直線 $m$ 上にあるかどうかをチェックしてみよう。点Bの $x$ 座標が13であり,$m:y=-3x+34$ に $x=13$ を代入すると
\begin{align*}
y=-3\times13+34=-5
\end{align*}
となり点Bの $y$ 座標に一致する。つまり,点Bは直線 $m$ 上にあることが分かる。y=-3\times13+34=-5
\end{align*}
(1)の結果より,この場合に $\text{AP}+\text{PQ}$ が最小になるのは,点Qが点B$(13,~-5)$ に一致するときである。このときの点Pの座標は $(4,~2)$ であり,$\text{AP}+\text{PQ}$ の最小値は $10\sqrt{2}$ である。
しかし「これは(2)の解ではないだろう」と思うはず。これが解なら簡単すぎるということになるし,今回の問題は空欄を埋めるタイプで,そもそも空欄に当てはまらないから解でないことが確定する。ということで,点Aを $l$ に関して対称移動させて考える。

$l$ に関して点Aと対称な点A$’$ を考えることで,
\begin{align*}
\text{AP}+\text{PQ}=\text{A}’\text{P}+\text{PQ}
\end{align*}
となる。折れ線A$’$PQの長さが最小になるような2点P,Qを考える。それは3点A$’$,P,Qが一直線上にあるときであるから\text{AP}+\text{PQ}=\text{A}’\text{P}+\text{PQ}
\end{align*}
\begin{align*}
\text{AP}+\text{PQ}\geqq\text{A}’\text{Q}
\end{align*}
が成り立つ。さらに,A$’$Qの長さが最小になるのは,A$’$Qと直線 $m$ が垂直になるときである。\text{AP}+\text{PQ}\geqq\text{A}’\text{Q}
\end{align*}
ゴールまでの道筋も見えたから,点A$’$ の座標を求めて解答を前進させよう。
点A$’$ の座標を $(X,~Y)$ とおくとAA$’$の中点が直線 $l$ 上にあるから
\begin{align*}
&\dfrac{Y+5}{2}=-\dfrac{1}{2}\Cdota\dfrac{X+3}{2}+4 \\[4pt]&X+2Y=3~\cdots\cdots①
\end{align*}
AA$’$ と $l$ が垂直であるから&\dfrac{Y+5}{2}=-\dfrac{1}{2}\Cdota\dfrac{X+3}{2}+4 \\[4pt]&X+2Y=3~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{Y-5}{X-3}\Cdota\left(-\dfrac{1}{2}\right)=-1 \\[4pt]&2X-Y=1~\cdots\cdots②
\end{align*}
①,②を解いて,$X=1,~Y=1$&\dfrac{Y-5}{X-3}\Cdota\left(-\dfrac{1}{2}\right)=-1 \\[4pt]&2X-Y=1~\cdots\cdots②
\end{align*}
よって,A$'(1,~1)$
次に,点A$’$ を通り,直線 $m$ に垂直な直線 $n$ の方程式を求める。$m$ の傾きは $-3$ であるから,$n$ の方程式は
\begin{align*}
&y=\dfrac{1}{3}(x-1)+1 \\[4pt]&y=\dfrac{1}{3}x+\dfrac{2}{3}
\end{align*}
点Pは2直線 $l,~n$ の交点であるから&y=\dfrac{1}{3}(x-1)+1 \\[4pt]&y=\dfrac{1}{3}x+\dfrac{2}{3}
\end{align*}
\begin{align*}
\begin{cases}
y=-\dfrac{1}{2}x+4 &\cdots\cdots③ \\[4pt]y=\dfrac{1}{3}x+\dfrac{2}{3} &\cdots\cdots④
\end{cases}
\end{align*}
を解く。③,④より $y$ を消去すると\begin{cases}
y=-\dfrac{1}{2}x+4 &\cdots\cdots③ \\[4pt]y=\dfrac{1}{3}x+\dfrac{2}{3} &\cdots\cdots④
\end{cases}
\end{align*}
\begin{align*}
&\dfrac{1}{3}x+\dfrac{2}{3}=-\dfrac{1}{2}x+4 \\[4pt]&\dfrac{5}{6}x=\dfrac{10}{3} \\[4pt]&x=4
\end{align*}
③より,$y=2$&\dfrac{1}{3}x+\dfrac{2}{3}=-\dfrac{1}{2}x+4 \\[4pt]&\dfrac{5}{6}x=\dfrac{10}{3} \\[4pt]&x=4
\end{align*}
よって,P$(4,~2)$ である。
また,点Qは2直線 $m,~n$ の交点であるから
\begin{align*}
\begin{cases}
y=\dfrac{1}{3}x+\dfrac{2}{3} &\cdots\cdots④ \\[4pt]y=-3x+34 &\cdots\cdots⑤
\end{cases}
\end{align*}
を解く。④,⑤より $y$ を消去すると\begin{cases}
y=\dfrac{1}{3}x+\dfrac{2}{3} &\cdots\cdots④ \\[4pt]y=-3x+34 &\cdots\cdots⑤
\end{cases}
\end{align*}
\begin{align*}
&\dfrac{1}{3}x+\dfrac{2}{3}=-3x+34 \\[4pt]&x+2=-9x+102 \\[4pt]&x=10
\end{align*}
⑤より,$y=4$&\dfrac{1}{3}x+\dfrac{2}{3}=-3x+34 \\[4pt]&x+2=-9x+102 \\[4pt]&x=10
\end{align*}
よって,Q$(10,~4)$ である。
したがって,$\text{AP}+\text{PQ}$ の最小値は
\begin{align*}
\text{A}’\text{Q}&=\sqrt{(10-1)^2+(4-1)^2} \\[4pt]&=\sqrt{90}=3\sqrt{10}
\end{align*}
「点と直線の距離の公式」を利用して次のように求めても良い。\text{A}’\text{Q}&=\sqrt{(10-1)^2+(4-1)^2} \\[4pt]&=\sqrt{90}=3\sqrt{10}
\end{align*}
点A$’$ と直線 $m:3x+y-34=0$ との距離を $d$ とすると
\begin{align*}
d&=\dfrac{\abs{3\Cdot1+1-34}}{\sqrt{3^2+1^2}} \\[4pt]&=\dfrac{30}{\sqrt{10}}=3\sqrt{10}
\end{align*}
d&=\dfrac{\abs{3\Cdot1+1-34}}{\sqrt{3^2+1^2}} \\[4pt]&=\dfrac{30}{\sqrt{10}}=3\sqrt{10}
\end{align*}




















