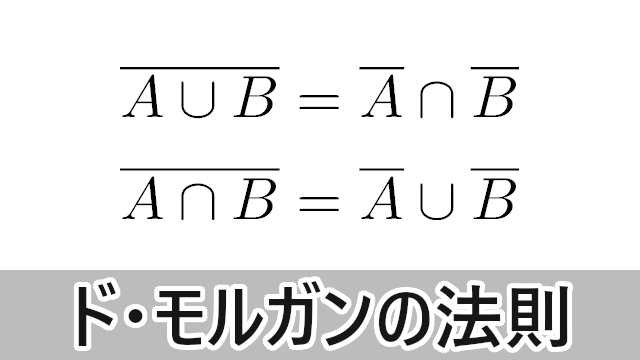ド・モルガンの法則について説明します。
定期テストでド・モルガンの法則を理解しているか確認するような問題が出題されても大丈夫なように対策をしておきましょう。
ド・モルガンの法則

ヒロ
まずはド・モルガンの法則がどのようなものかを知ろう。

ヒロ
ド・モルガンの法則は2つの集合の和集合・共通部分の補集合についての法則で次のようになっている。
ド・モルガンの法則$A\cup B$,$A\cap B$ の補集合について次の法則が成り立つ。
\begin{align*}
&\overline{A\cup B}=\overline{A}\cap\overline{B} \\[4pt]
&\overline{A\cap B}=\overline{A}\cup\overline{B}
\end{align*}
&\overline{A\cup B}=\overline{A}\cap\overline{B} \\[4pt]
&\overline{A\cap B}=\overline{A}\cup\overline{B}
\end{align*}

ヒロ
ド・モルガンの法則が成り立つことをベン図を利用して確認しておこう。
【ド・モルガンの法則が成り立つことの確認】
$\overline{A}$ が表す部分は次の図の斜線部分。

$\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}\cap\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}\cup\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}$ と $\overline{B}$ の共通部分が $\overline{A}\cap\overline{B}$ になっていることが分かるだろう。
また $\overline{A}$ と $\overline{B}$ の和集合が $\overline{A}\cup\overline{B}$ になっていることも分かるだろう。
$\overline{A}$ が表す部分は次の図の斜線部分。

$\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}\cap\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}\cup\overline{B}$ が表す部分は次の図の斜線部分。

$\overline{A}$ と $\overline{B}$ の共通部分が $\overline{A}\cap\overline{B}$ になっていることが分かるだろう。
また $\overline{A}$ と $\overline{B}$ の和集合が $\overline{A}\cup\overline{B}$ になっていることも分かるだろう。
「かつ」と「または」

ヒロ
このド・モルガンの法則を使いこなせることが重要だけど丸覚えでは,3か月もしたら忘れてしまうだろう。

ヒロ
ベン図を利用して一度理解してしまえば,同じようにしてド・モルガンの法則を使えるようにはなるが,もっと機械的にしたいのが本音。

ヒロ
ということで,その方法をマスターしよう。
【共通部分と和集合の言い換え】
$A\cap B$ は $A$ と $B$ のどちらにも属する部分を表すから「$A$ に属するかつ $B$ に属する」ということができる。
また $A\cup B$ は $A$ と $B$ の少なくとも一方に属する部分を表すから「$A$ に属するまたは $B$ に属する」ということができる。
$A\cap B$ は $A$ と $B$ のどちらにも属する部分を表すから「$A$ に属するかつ $B$ に属する」ということができる。
また $A\cup B$ は $A$ と $B$ の少なくとも一方に属する部分を表すから「$A$ に属するまたは $B$ に属する」ということができる。
【ド・モルガンの法則】
$\overline{A\cap B}$ は $A\cap B$ の否定と考えて,1つずつ否定にしていく。
「かつ $\cap$」の否定が「または $\cup$」と考えると
$\overline{A\cap B}$ は $A\cap B$ の否定と考えて,1つずつ否定にしていく。
「かつ $\cap$」の否定が「または $\cup$」と考えると
\begin{align*}
\overline{A\cap B}=\overline{A}\cup\overline{B}
\end{align*}
となる。同じように $\overline{A\cup B}$ も\overline{A\cap B}=\overline{A}\cup\overline{B}
\end{align*}
\begin{align*}
\overline{A\cup B}=\overline{A}\cap\overline{B}
\end{align*}
となる。\overline{A\cup B}=\overline{A}\cap\overline{B}
\end{align*}

ヒロ
これで特に考えることもなく変形することができるね。

ヒロ
ちなみに $\cap$ と $\cup$ のどちらが「かつ」になるかは「且つ」という漢字を想像すれば,その形から $\cap$ が「かつ」であると覚えることができる。
ド・モルガンの法則を利用する問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題$U=\{x\mid 0<=x<13,~x~は整数\}$ が全体集合となる とき,$A=\{x\mid x~は5の倍数\}$,$B=\{x\mid x~は12の正の約数\}$ と する。次の集合を求めよ。
(1) $\overline{B}$
(2) $\overline{A}\cup\overline{B}$
(1) $\overline{B}$
(2) $\overline{A}\cup\overline{B}$

ヒロ
(1)は13未満の自然数のうち,12の約数でないものを書けば良いね。
【(1)の解答】
12の正の約数は
12の正の約数は
\begin{align*} 1,~2,~3,~4,~6,~12 \end{align*}
であるから \begin{align*} \overline{B}=\{5,~7,~8,~9,~10,~11\} \end{align*}

ヒロ
(2)はそのまま考えても良いが,練習のためにド・モルガンの法則を使って考えてみよう。
【(2)の解答】
ド・モルガンの法則より
ド・モルガンの法則より
\begin{align*} \overline{A}\cup\overline{B}=\overline{A\cap B} \end{align*}
ここで $A\cap B$ は13未満の自然数のうち,5の倍数で,かつ12の約数の集合である が,そのような数は存在しないので空集合 $\emptyset$ である。$\overline{\emptyset}=U$ であるから \begin{align*} \overline{A}\cup\overline{B}=U \end{align*}