Contents
弦の長さを求める方法

ヒロ
弦の長さを求める方法を知ろう。
三平方の定理を利用する

ヒロ
弦の長さを求める問題は高校入試でも出題されるが,そのときに用いた解法が「三平方の定理を利用する方法」である。
次の図のように,円 $C$ と直線 $l$ が2点P,Qで交わっているとする。
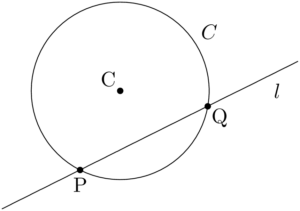
直線 $l$ が円 $C$ から切り取られる線分(弦PQ)の長さを求めるために。円の中心Cから直線 $l$ に垂線CHを下ろす。$\sankaku{CPQ}$ は $\text{CP}=\text{CQ}$ の二等辺三角形であるから,点Hは線分PQの中点である。
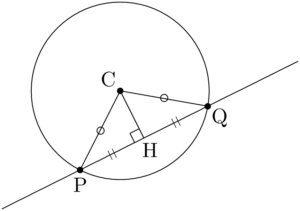
$\sankaku{CPH}$ において,CPの長さは円 $C$ の半径 $r$ である。また,CHの長さは点Cと直線 $l$ の距離 $d$ である。
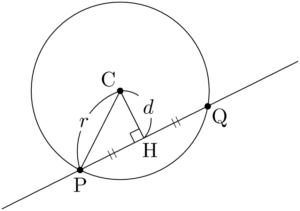
三平方の定理より
\begin{align*}
\text{PH}&=\sqrt{\text{CP}^2-\text{CH}^2} \\[4pt]
&=\sqrt{r^2-d^2}
\end{align*}
となるから,求める弦PQの長さは\text{PH}&=\sqrt{\text{CP}^2-\text{CH}^2} \\[4pt]
&=\sqrt{r^2-d^2}
\end{align*}
\begin{align*}
\text{PQ}&=2\text{PH} \\[4pt]
&=2\sqrt{r^2-d^2}
\end{align*}
\text{PQ}&=2\text{PH} \\[4pt]
&=2\sqrt{r^2-d^2}
\end{align*}
交点の座標を利用する

ヒロ
円 $C$ と直線 $l$ の2つの交点P,Qの座標を求めることで,弦PQの長さを2点P,Q間の距離として求めることができる。

ヒロ
この方法のデメリットとしては,2つの交点の座標を求める計算が面倒なことだろう。

ヒロ
ただし,問題によっては2つの交点の座標を求めさせることもあるため,そのような問題に対しては,その流れで2点間の距離を求めることで弦の長さを求めればよい。

ヒロ
交点の座標を利用するなら,次の考え方を知っておくと良いだろう。
【交点の座標をうまく利用する】
円 $C$ と $y$ 軸に平行でない直線 $l$ が2点P,Qで交わっているときを考える。

ここで,$l$ の傾きを $m$ とし,2点P,Qの $x$ 座標をそれぞれ $p,~q$ とする。また,点Pから直線 $x=q$ に下ろした垂線の足をHとする。
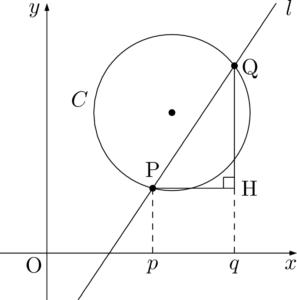
PQを斜辺とする直角三角形 $\sankaku{PQH}$ に着目する。直線 $l$ の傾きが $m$ であるから,
\begin{align*}
\text{PH}:\text{QH}=1:m
\end{align*}
が成り立つ。これより\text{PH}:\text{QH}=1:m
\end{align*}
\begin{align*}
\text{PH}:\text{PQ}=1:\sqrt{m^2+1}
\end{align*}
となる。\text{PH}:\text{PQ}=1:\sqrt{m^2+1}
\end{align*}
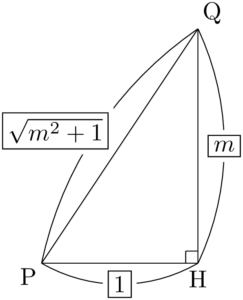
したがって,弦PQの長さは
\begin{align*}
\text{PQ}&=\sqrt{m^2+1}\,\text{PH} \\[4pt]
&=(q-p)\sqrt{m^2+1}
\end{align*}
\text{PQ}&=\sqrt{m^2+1}\,\text{PH} \\[4pt]
&=(q-p)\sqrt{m^2+1}
\end{align*}

ヒロ
この考え方を利用することで,2点P,Qの $x$ 座標を求めた後,$y$ 座標を求める必要がなくなるため,計算が少し楽になるだろう。


















