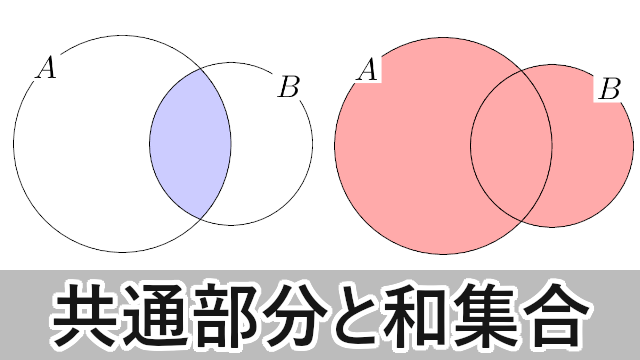
ここでは集合の共通部分と和集合について説明します。
いくつかの集合を扱うときに,複数の集合に属する要素が存在することがあります。
そのような複数の集合の共通部分だけを表す方法と複数の集合全体を表す方法について説明します。
集合の共通部分と和集合

ヒロ
集合の共通部分と和集合を表す記号を知っておこう。
集合の共通部分2つの集合 $A,~B$ に対して,$A$ と $B$ のどちらにも属する要素全体の集合を $A$ と $B$ の共通部分といい,$A\cap B$ で表す。つまり

\begin{align*}
A\cap B=\{x\mid x\in A~かつ~x\in B\}
\end{align*}
ということである。A\cap B=\{x\mid x\in A~かつ~x\in B\}
\end{align*}

和集合2つの集合 $A,~B$ に対して,$A$ と $B$ の少なくとも一方に属する要素全体の集合を $A$ と $B$ の和集合といい,$A\cup B$ で表す。つまり

\begin{align*}
A\cup B=\{x\mid x\in A~または~x\in B\}
\end{align*}
ということである。A\cup B=\{x\mid x\in A~または~x\in B\}
\end{align*}

集合の共通部分と和集合に関する問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題$A=\{n\mid n~は16の正の約数\}$,$B=\{n\mid n~は20の正の約数\}$,$C=\{n\mid n~は8以下の正の偶数\}$ とする。このとき,次の集合を求めよ。
(1) $A\cap B$
(2) $B\cup C$
(3) $(A\cap C)\cup(B\cap C)$
(1) $A\cap B$
(2) $B\cup C$
(3) $(A\cap C)\cup(B\cap C)$

ヒロ
(1)は $A$ と $B$ の集合の要素がどうなっているかを調べよう。
【(1)の考え方と解答】
\begin{align*}
&A=\{1,~2,~4,~8,~16\} \\[4pt]
&B=\{1,~2,~4,~5,~10,~20\}
\end{align*}
$A\cap B$ は $A$ と $B$ の共通部分を表すから,$A$ と $B$ に共通する要素だけを書くようにしよう。&A=\{1,~2,~4,~8,~16\} \\[4pt]
&B=\{1,~2,~4,~5,~10,~20\}
\end{align*}
\begin{align*}
A\cap B=\{1,~2,~4\}
\end{align*}
A\cap B=\{1,~2,~4\}
\end{align*}

ヒロ
(2)は $B$ と $C$ の集合の要素がどうなっているかを調べよう。
【(2)の考え方と解答】
$C=\{2,~4,~6,~8\}$ であり,$B\cup C$ は $B$ と $C$ の和集合を表すから,$B$ と $C$ に属する要素をすべて書くようにしよう。ただし,両方の集合の要素でも1つだけ書くようにしよう。
$C=\{2,~4,~6,~8\}$ であり,$B\cup C$ は $B$ と $C$ の和集合を表すから,$B$ と $C$ に属する要素をすべて書くようにしよう。ただし,両方の集合の要素でも1つだけ書くようにしよう。
\begin{align*}
B\cup C=\{1,~2,~4,~5,~6,~8,~10,~20\}
\end{align*}
B\cup C=\{1,~2,~4,~5,~6,~8,~10,~20\}
\end{align*}

ヒロ
1つずつ丁寧に考えよう。
【(3)の考え方と解答】
1つずつ丁寧に考えよう。$A$ と $C$ の共通部分を考えて
1つずつ丁寧に考えよう。$A$ と $C$ の共通部分を考えて
\begin{align*}
A\cap C=\{2,~4,~8\}
\end{align*}
$B$ と $C$ の共通部分を考えてA\cap C=\{2,~4,~8\}
\end{align*}
\begin{align*}
B\cap C=\{2,~4\}
\end{align*}
求めるものは $A\cap C$ と $B\cap C$ の和集合であるからB\cap C=\{2,~4\}
\end{align*}
\begin{align*}
\{2,~4,~8\}
\end{align*}
\{2,~4,~8\}
\end{align*}
集合の共通部分と和集合に関する問題2

ヒロ
次の問題を解いてみよう。
問題$A=\{1,~3,~3a-2\}$,$B=\{-5,~a+2,~a^2-2a+1\}$,$A\cap B=\{1,~4\}$ のとき,定数 $a$ の値と和集合 $A\cup B$ を求めよ。

ヒロ
要素に文字が使われているので,落ち着いて考えよう。
【考え方と解答】
2つの集合 $A$ と $B$ の共通部分に着目しよう。
共通部分が1と4であることから,2つの集合に1と4が含まれていることが分かる。
この時点で,集合 $A$ の要素である $3a-2$ が4であることが分かる。
2つの集合 $A$ と $B$ の共通部分に着目しよう。
共通部分が1と4であることから,2つの集合に1と4が含まれていることが分かる。
この時点で,集合 $A$ の要素である $3a-2$ が4であることが分かる。
\begin{align*}
&3a-2=4 \\[4pt]
&a=2
\end{align*}
$a$ の値が分かったから要素がどうなっているかが分かる。&3a-2=4 \\[4pt]
&a=2
\end{align*}
\begin{align*}
&A=\{1,~3,~4\} \\[4pt]
&B=\{-5,~4,~1\}
\end{align*}
したがって,和集合は&A=\{1,~3,~4\} \\[4pt]
&B=\{-5,~4,~1\}
\end{align*}
\begin{align*}
A\cup B=\{-5,~1,~3,~4\}
\end{align*}
A\cup B=\{-5,~1,~3,~4\}
\end{align*}
3つの集合の共通部分と和集合

ヒロ
3つの集合の共通部分と和集合についても知っておこう。
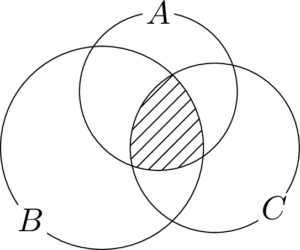
共通部分と和集合3つの集合 $A,~B,~C$ に対して,$A,~B,~C$ のどれにも属する要素全体の集合を $A,~B,~C$ の共通部分といい,$A\cap B\cap C$ で表す。つまり
また,$A,~B,~C$ の少なくとも1つに属する要素全体の集合を $A,~B,~C$ の和集合といい,$A\cup B\cup C$ で表す。つまり
\begin{align*}
A\cap B\cap C=\{x\mid x\in A~かつ~x\in B~かつ~x\in C\}
\end{align*}
ということである。A\cap B\cap C=\{x\mid x\in A~かつ~x\in B~かつ~x\in C\}
\end{align*}

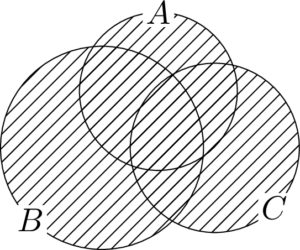
また,$A,~B,~C$ の少なくとも1つに属する要素全体の集合を $A,~B,~C$ の和集合といい,$A\cup B\cup C$ で表す。つまり
\begin{align*}
A\cup B\cup C=\{x\mid x\in A~または~x\in B~または~x\in C\}
\end{align*}
ということである。A\cup B\cup C=\{x\mid x\in A~または~x\in B~または~x\in C\}
\end{align*}

集合の共通部分と和集合に関する問題3

ヒロ
次の問題を解いてみよう。
問題$A=\{1,~2,~3,~4,~5\}$,$B=\{2,~3,~5,~7\}$,$C=\{1,~2,~4,~8\}$ について,次の集合を求めよ。
(1) $A\cap B\cap C$
(2) $A\cup B\cup C$
(1) $A\cap B\cap C$
(2) $A\cup B\cup C$

ヒロ
落ち着いて要素を見れば大丈夫だろう。
【解答】
(1) 3つの集合の共通部分を考えて $\{2\}$
(2) 3つの集合の和集合を考えて $\{1,~2,~3,~4,~5,~7,~8\}$
(1) 3つの集合の共通部分を考えて $\{2\}$
(2) 3つの集合の和集合を考えて $\{1,~2,~3,~4,~5,~7,~8\}$