Contents
弦の長さを求める問題【東京電機大】
2008年 東京電機大円 $(x-2)^2+(y-1)^2=4$ と直線 $y=-2x+3$ の2つの交点をA,Bとするとき,弦ABの長さを求めよ。
【考え方と解答】
円の中心 $(2,~1)$ と直線 $2x+y-3=0$ との距離を $d$ とすると
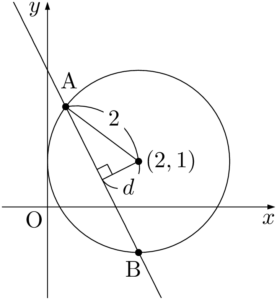
円の半径が2であるから,
円の中心 $(2,~1)$ と直線 $2x+y-3=0$ との距離を $d$ とすると
\begin{align*}
d&=\dfrac{\abs{2\Cdot2+1-3}}{\sqrt{2^2+1^2}} \\[4pt]
&=\dfrac{2}{\sqrt{5}}
\end{align*}
d&=\dfrac{\abs{2\Cdot2+1-3}}{\sqrt{2^2+1^2}} \\[4pt]
&=\dfrac{2}{\sqrt{5}}
\end{align*}

円の半径が2であるから,
\begin{align*}
\text{AB}&=2\sqrt{2^2-d^2} \\[4pt]
&=2\sqrt{4-\dfrac{4}{5}} \\[4pt]
&=\dfrac{8}{\sqrt{5}}=\dfrac{8\sqrt{5}}{5}
\end{align*}
\text{AB}&=2\sqrt{2^2-d^2} \\[4pt]
&=2\sqrt{4-\dfrac{4}{5}} \\[4pt]
&=\dfrac{8}{\sqrt{5}}=\dfrac{8\sqrt{5}}{5}
\end{align*}
弦の長さに関する問題【東洋大】
2015年 東洋大直線 $y=mx+4$($m$ は正の定数)が円 $x^2+y^2=36$ によって切りとられる弦の長さが $4\sqrt{6}$ のとき,$m=\dfrac{\sqrt{\myhako}}{\myhako}$ である。
【考え方と解答】
円 $x^2+y^2=36$ の中心と直線 $y=mx+4$ の距離を $d$ とすると
円 $x^2+y^2=36$ の中心と直線 $y=mx+4$ の距離を $d$ とすると
\begin{align*}
d=\dfrac{4}{\sqrt{m^2+1}}~\cdots\cdots①
\end{align*}
円の半径は6であり,弦の長さが $4\sqrt{6}$ であるからd=\dfrac{4}{\sqrt{m^2+1}}~\cdots\cdots①
\end{align*}
\begin{align*}
&2\sqrt{6^2-d^2}=4\sqrt{6} \\[4pt]
&\sqrt{36-d^2}=2\sqrt{6}
\end{align*}
両辺を2乗すると&2\sqrt{6^2-d^2}=4\sqrt{6} \\[4pt]
&\sqrt{36-d^2}=2\sqrt{6}
\end{align*}
\begin{align*}
&36-d^2=24 \\[4pt]
&d^2=12
\end{align*}
①より&36-d^2=24 \\[4pt]
&d^2=12
\end{align*}
\begin{align*}
&\dfrac{16}{m^2+1}=12 \\[4pt]
&m^2+1=\dfrac{4}{3} \\[4pt]
&m^2=\dfrac{1}{3} \\[4pt]
&m=\pm\dfrac{1}{\sqrt{3}}
\end{align*}
$m>0$ より,$m=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$&\dfrac{16}{m^2+1}=12 \\[4pt]
&m^2+1=\dfrac{4}{3} \\[4pt]
&m^2=\dfrac{1}{3} \\[4pt]
&m=\pm\dfrac{1}{\sqrt{3}}
\end{align*}


















