ここでは直線に関して対称な点について説明します。
大学入試では,単に直線に関して対称な点を求めるだけでなく,求めることを前提にした問題もあるため,直線に関して対称な点の求め方や性質をしっかり理解することが重要です。
Contents
直線に関して対称な点

ヒロ
直線に関して対称な点の座標を求められるようにしよう。
x軸に平行な直線に関して対称な点

ヒロ
まずは $x$ 軸に平行な直線($y$ 軸に垂直な直線)に関して対称な点の座標を求められるようにしよう。
【$x$ 軸に平行な直線に関して対称な点】
直線 $y=a$ に関して,点P$(p,~q)$ と対称な点をQとする。
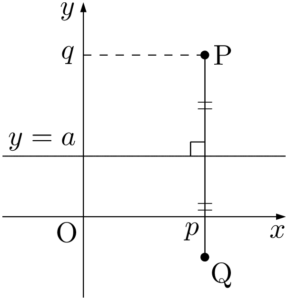
点Qの $x$ 座標は $p$ であることは簡単に分かるから,$y$ 座標を考える。線分PQの中点が直線 $y=a$ 上にあるから,Qの $y$ 座標を $Y$ とすると
直線 $y=a$ に関して,点P$(p,~q)$ と対称な点をQとする。

点Qの $x$ 座標は $p$ であることは簡単に分かるから,$y$ 座標を考える。線分PQの中点が直線 $y=a$ 上にあるから,Qの $y$ 座標を $Y$ とすると
\begin{align*}
&\dfrac{q+Y}{2}=a \\[4pt]
&Y=2a-q
\end{align*}
したがって,Q $(a,~2a-q)$ である。&\dfrac{q+Y}{2}=a \\[4pt]
&Y=2a-q
\end{align*}
y軸に平行な直線に関して対称な点

ヒロ
$y$ 軸に平行な直線($x$ 軸に垂直な直線)に関して対称な点の座標を求められるようにしよう。
【$y$ 軸に平行な直線に関して対称な点】
直線 $x=a$ に関して,点P$(p,~q)$ と対称な点をQとする。
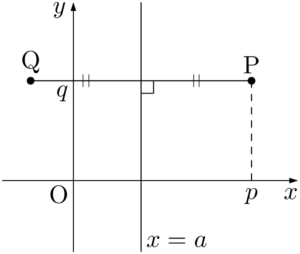
点Qの $y$ 座標は $q$ であることは簡単に分かるから,$x$ 座標を考える。線分PQの中点が直線 $x=a$ 上にあるから,Qの $x$ 座標を $X$ とすると
直線 $x=a$ に関して,点P$(p,~q)$ と対称な点をQとする。

点Qの $y$ 座標は $q$ であることは簡単に分かるから,$x$ 座標を考える。線分PQの中点が直線 $x=a$ 上にあるから,Qの $x$ 座標を $X$ とすると
\begin{align*}
&\dfrac{p+X}{2}=a \\[4pt]
&X=2a-p
\end{align*}
したがって,Q $(2a-p,~q)$ である。&\dfrac{p+X}{2}=a \\[4pt]
&X=2a-p
\end{align*}
座標軸に平行でない直線に関して対称な点

ヒロ
それでは座標軸に平行でない直線に関して対称な点の座標を求めよう。
【座標軸に平行でない直線に関して対称な点】
直線 $l:ax+by+c=0~(a\neq0,~b\neq0)$ に関して,点P$(p,~q)$ と対称な点をQ$(X,~Y)$ とし,線分PQと直線 $l$ の交点をHとする。
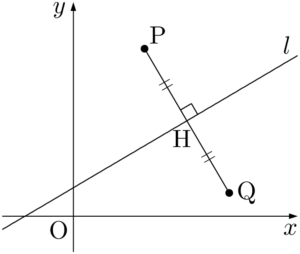
点Qの座標を求めるためには,2つの方程式が必要となる。点Qが直線 $l$ に関して点Pと対称な点であるとき,次の2つの条件をみたす。
直線 $l:ax+by+c=0~(a\neq0,~b\neq0)$ に関して,点P$(p,~q)$ と対称な点をQ$(X,~Y)$ とし,線分PQと直線 $l$ の交点をHとする。

点Qの座標を求めるためには,2つの方程式が必要となる。点Qが直線 $l$ に関して点Pと対称な点であるとき,次の2つの条件をみたす。
- 線分PQの中点が直線 $l$ 上にある
- PQ $\perp l$
それぞれの条件から方程式を立てよう。
線分PQの中点は点Hで,その座標は $\left(\dfrac{p+X}{2},~\dfrac{q+Y}{2}\right)$ であり,点Hが直線 $l$ 上にあるから
\begin{align*}
&a\Cdota\dfrac{p+X}{2}+b\Cdota\dfrac{q+Y}{2}+c=0 \\[4pt]
&aX+bY=-ap-bq-2c~\cdots\cdots①
\end{align*}
また,直線PQの傾きは $\dfrac{Y-q}{X-p}$ であり,$l$ の傾きは $-\dfrac{a}{b}$ であるから&a\Cdota\dfrac{p+X}{2}+b\Cdota\dfrac{q+Y}{2}+c=0 \\[4pt]
&aX+bY=-ap-bq-2c~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{Y-q}{X-p}\Cdota\left(-\dfrac{a}{b}\right)=-1 \\[4pt]
&a(Y-q)=b(X-p) \\[4pt]
&bX-aY=bp-aq~\cdots\cdots②
\end{align*}
$①\times a+②\times b$ より&\dfrac{Y-q}{X-p}\Cdota\left(-\dfrac{a}{b}\right)=-1 \\[4pt]
&a(Y-q)=b(X-p) \\[4pt]
&bX-aY=bp-aq~\cdots\cdots②
\end{align*}
\begin{align*}
(a^2+b^2)X&=(-a^2+b^2)p-2abq-2ca \\[4pt]
&(a^2+b^2)p-2a(ap+bq+c)
\end{align*}
$a^2+b^2\neq0$ であるから(a^2+b^2)X&=(-a^2+b^2)p-2abq-2ca \\[4pt]
&(a^2+b^2)p-2a(ap+bq+c)
\end{align*}
\begin{align*}
X=p-\dfrac{2a(ap+bq+c)}{a^2+b^2}
\end{align*}
$①\times b-②\times a$ よりX=p-\dfrac{2a(ap+bq+c)}{a^2+b^2}
\end{align*}
\begin{align*}
(a^2+b^2)Y&=-2abp+(a^2-b^2)q-2bc \\[4pt]
&(a^2+b^2)q-2b(ap+bq+c)
\end{align*}
$a^2+b^2\neq0$ であるから(a^2+b^2)Y&=-2abp+(a^2-b^2)q-2bc \\[4pt]
&(a^2+b^2)q-2b(ap+bq+c)
\end{align*}
\begin{align*}
Y=q-\dfrac{2b(ap+bq+c)}{a^2+b^2}
\end{align*}
よって,点Qの座標はY=q-\dfrac{2b(ap+bq+c)}{a^2+b^2}
\end{align*}
\begin{align*}
\text{Q}\left(p-\dfrac{2a(ap+bq+c)}{a^2+b^2},~q-\dfrac{2b(ap+bq+c)}{a^2+b^2}\right)
\end{align*}
\text{Q}\left(p-\dfrac{2a(ap+bq+c)}{a^2+b^2},~q-\dfrac{2b(ap+bq+c)}{a^2+b^2}\right)
\end{align*}


















