Contents
直線に関して対称な点を求める問題【津田塾大】
2015年 津田塾大平面上の直線 $y=\dfrac{1}{2}x+1$ に関して点$(2,~7)$ と対称な点の座標を求めよ。
【考え方と解答】
直線 $y=\dfrac{1}{2}x+1$ を $l$ とし,点$(2,~7)$ をAとする。求める点をB$(p,~q)$ とおくと,
よって,求める点の座標は $(6,~-1)$
直線 $y=\dfrac{1}{2}x+1$ を $l$ とし,点$(2,~7)$ をAとする。求める点をB$(p,~q)$ とおくと,
\begin{align*}
&\text{線分ABの中点が}l\text{上にある}~\cdots\cdots① \\[4pt]
&\text{AB}\perp l~\cdots\cdots②
\end{align*}
線分ABの中点は $\left(\dfrac{2+p}{2},~\dfrac{7+q}{2}\right)$ であるから,①より&\text{線分ABの中点が}l\text{上にある}~\cdots\cdots① \\[4pt]
&\text{AB}\perp l~\cdots\cdots②
\end{align*}
\begin{align*}
&\dfrac{7+q}{2}=\dfrac{1}{2}\Cdota\dfrac{2+p}{2}+1 \\[4pt]
&14+2q=2+p+4 \\[4pt]
&p-2q=8~\cdots\cdots①’
\end{align*}
$p=2$ のときは条件をみたさないから,$p\neq2$ である。ABの傾きは $\dfrac{q-7}{p-2}$ であるから,②より&\dfrac{7+q}{2}=\dfrac{1}{2}\Cdota\dfrac{2+p}{2}+1 \\[4pt]
&14+2q=2+p+4 \\[4pt]
&p-2q=8~\cdots\cdots①’
\end{align*}
\begin{align*}
&\dfrac{q-7}{p-2}\Cdota\dfrac{1}{2}=-1 \\[4pt]
&q-7=-2p+4 \\[4pt]
&2p+q=11~\cdots\cdots②’
\end{align*}
$①’,~②’$ より,$p=6,~q=-1$&\dfrac{q-7}{p-2}\Cdota\dfrac{1}{2}=-1 \\[4pt]
&q-7=-2p+4 \\[4pt]
&2p+q=11~\cdots\cdots②’
\end{align*}
よって,求める点の座標は $(6,~-1)$
覚えた方が良い対称移動

ヒロ
津田塾大の問題を通して,直線に関して対称な点の座標の求め方については理解できただろう。

ヒロ
しかし,有名な対称移動を覚えておくことで「答えだけを求めれば良い問題」では,ほとんど計算することなく答えを求めることができるようになる。
直線 y=x に関して対称な点
【直線 $l:y=x$ に関する対称移動】
点A$(a,~b)$ の直線 $l$ に関して対称な点をB$(X,~Y)$ とする。
ABの中点が $l$ 上にあるから
よって,B$(b,~a)$ である。
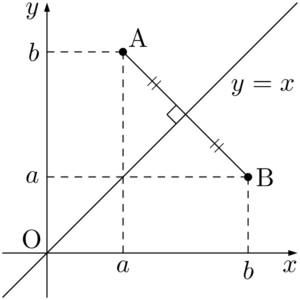
点A$(a,~b)$ の直線 $l$ に関して対称な点をB$(X,~Y)$ とする。
ABの中点が $l$ 上にあるから
\begin{align*}
&\dfrac{a+X}{2}=\dfrac{b+Y}{2} \\[4pt]
&X-Y=-a+b~\cdots\cdots①
\end{align*}
ABと $l$ が垂直であるから&\dfrac{a+X}{2}=\dfrac{b+Y}{2} \\[4pt]
&X-Y=-a+b~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{Y-b}{X-a}\Cdota1=-1 \\[4pt]
&Y-b=-X+a \\[4pt]
&X+Y=a+b~\cdots\cdots②
\end{align*}
①,②より,$X=b,~Y=a$&\dfrac{Y-b}{X-a}\Cdota1=-1 \\[4pt]
&Y-b=-X+a \\[4pt]
&X+Y=a+b~\cdots\cdots②
\end{align*}
よって,B$(b,~a)$ である。


ヒロ
直線 $y=x$ に関して対称移動するときは,$x$ 座標と $y$ 座標を入れ換えるだけで良いことが分かる。
直線 y=-x に関して対称な点
【直線 $l:y=-x$ に関する対称移動】
点A$(a,~b)$ の直線 $l$ に関して対称な点をB$(X,~Y)$ とする。
ABの中点が $l$ 上にあるから
よって,B$(-b,~-a)$ である。
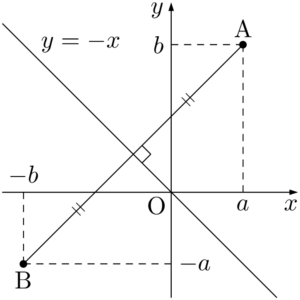
点A$(a,~b)$ の直線 $l$ に関して対称な点をB$(X,~Y)$ とする。
ABの中点が $l$ 上にあるから
\begin{align*}
&\dfrac{a+X}{2}=-\dfrac{b+Y}{2} \\[4pt]
&X+Y=-a-b~\cdots\cdots①
\end{align*}
ABと $l$ が垂直であるから&\dfrac{a+X}{2}=-\dfrac{b+Y}{2} \\[4pt]
&X+Y=-a-b~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{Y-b}{X-a}\Cdota(-1)=-1 \\[4pt]
&Y-b=X-a \\[4pt]
&X-Y=a-b~\cdots\cdots②
\end{align*}
①,②より,$X=-b,~Y=-a$&\dfrac{Y-b}{X-a}\Cdota(-1)=-1 \\[4pt]
&Y-b=X-a \\[4pt]
&X-Y=a-b~\cdots\cdots②
\end{align*}
よって,B$(-b,~-a)$ である。


ヒロ
直線 $y=-x$ に関して対称移動するときは,$x$ 座標と $y$ 座標を入れ換えて符号を変えれば良いことが分かる。

ヒロ
このことを常識にしておくと,マーク式試験や空欄を埋めるだけの問題においては一瞬で答えを求めることができる。



















