Contents
係数の和を求めていることに気付いていない

ヒロ
ということで,もう1問考えてもらおう。
補題22次関数 $y=ax^2+bx+c$ のグラフが下図のようになるとき,次の値の符号を調べよ。
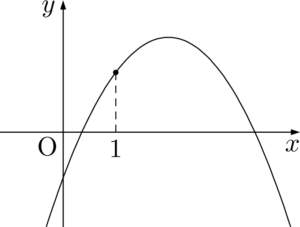
\begin{align*}
&(1)\ a+b+c \\[4pt]
&(2)\ a-b+c \\[4pt]
&(3)\ 4a-2b+c
\end{align*}
&(1)\ a+b+c \\[4pt]
&(2)\ a-b+c \\[4pt]
&(3)\ 4a-2b+c
\end{align*}


(1) は正ですね!

ヒロ
正解!どうやって考えたの?

$x=1$ を代入すると,$y=a+b+c$ になるから,グラフを見て正だと分かりました。

ヒロ
完璧だね!でも,何か気付かない?

え?何か変なこと言いました?

ヒロ
与えられている関数は,$y=ax^2+bx+c$ で求めるものは $a+b+c$ の符号。これってこの関数の・・・

あっ!係数の和なんですね!

ヒロ
そういうこと。係数の和を考えているのに,そのことに気付いていないんだよね。しかも,係数の和の求め方も知ってるはずなのに,それも当然気付いていない。


















