文字係数の3次関数の最大値と最小値に関する問題を解説します。
係数に文字が含まれているため,文字の値によって,最大値や最小値をとる $x$ の値が変化します。
うまく場合分けをして,最大値や最小値を求められるようにしましょう。
また,場合分けの際には,3次関数のグラフの等間隔性や対称性を知っていると良いかもしれません。
Contents
2021年 摂南大
2021年 摂南大$a$ を定数とする。3次関数 $y=x(x-3a)^2$ の $0\leqq x\leqq1$ における最大値を $M(a)$ とする。
(1) $a\neq0$ とする。このとき $f'(x)=0$ の解は $a$ と $\myhako\,a$ であり,$f(x)=f(a)$ の解は2重解 $a$ と $\myhako\,a$ である。
(2) $a<\myBox{ア}$,または $\myBox{イ}<a$ のとき,$M(a)=\myhako\,a^2-\myhako\,a+\myhako$ である。$\myBox{ア}\leqq a\leqq\myBox{イ}$ のとき,$M(a)=\myhako\,a^{\myhako}$ である。
(1) $a\neq0$ とする。このとき $f'(x)=0$ の解は $a$ と $\myhako\,a$ であり,$f(x)=f(a)$ の解は2重解 $a$ と $\myhako\,a$ である。
(2) $a<\myBox{ア}$,または $\myBox{イ}<a$ のとき,$M(a)=\myhako\,a^2-\myhako\,a+\myhako$ である。$\myBox{ア}\leqq a\leqq\myBox{イ}$ のとき,$M(a)=\myhako\,a^{\myhako}$ である。
【(1)の解答と考え方】
$f(x)=x^3-6ax^2+9a^2x$ より
$f(x)=x^3-6ax^2+9a^2x$ より
\begin{align*} f'(x)&=3x^2-12ax+9a^2 \\[4pt] &=3(x^2-4ax+3a^2) \\[4pt] &=3(x-a)(x-3a) \end{align*}
$f'(x)=0$ を解くと $x=a,~3a$ $f(x)=f(a)$ より\begin{align*} &x^3-6ax^2+9a^2x=a(a-3a)^2 \\[4pt] &x^3-6ax^2+9a^2x-4a^3=0 \end{align*}
通常なら,ここから因数定理を利用して因数分解するが,今回は「$f(x)=f(a)$ の解は2重解 $a$」と書かれているため,上の方程式の左辺が $(x-a)^2$ を因数にもつことが分かる。これを利用すると,定数項に着目するだけで簡単に因数分解できる。\begin{align*} &(x-a)^2(x-4a)=0 \end{align*}
よって,解は2重解 $a$ と $4a$ である。(2) $a<\myBox{ア}$,または $\myBox{イ}<a$ のとき,$M(a)=\myhako\,a^2-\myhako\,a+\myhako$ である。$\myBox{ア}\leqq a\leqq\myBox{イ}$ のとき,$M(a)=\myhako\,a^{\myhako}$ である。
【(2)の解答と考え方】
(1)の計算から,$y=x(x-3a)^2$ のグラフは $a$ の符号に応じて,次のような概形になることが分かる。$a$ が正の場合が左,$a$ が負の場合が右である。
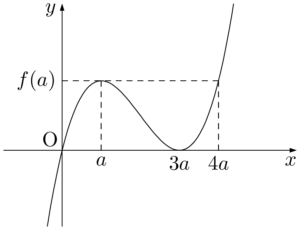
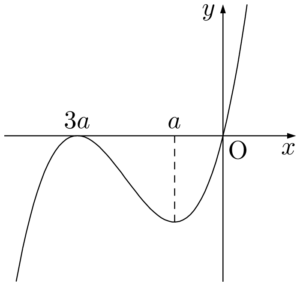
上の2つのグラフを見て,$0\leqq x\leqq1$ における最大値を考えると,$a<0$ の場合は,$x=1$ において $y$ が最大になることが分かるだろう。また,$a>0$ の場合は,極大で最大になるとは限らないことも分かるだろう。極大で最大となるのは,$f(4a)=f(a)$ であることを考えると,$a\leqq1\leqq4a$ すなわち $\dfrac{1}{4}\leqq a\leqq1$ のときであると分かるだろう。ここまで考えると,$\dfrac{1}{4}<a$ のときは,$x=1$ で最大となることも分かる。
したがって,$a<0$ または $\dfrac{1}{4}<a$ のとき,最大値は
(1)の計算から,$y=x(x-3a)^2$ のグラフは $a$ の符号に応じて,次のような概形になることが分かる。$a$ が正の場合が左,$a$ が負の場合が右である。


上の2つのグラフを見て,$0\leqq x\leqq1$ における最大値を考えると,$a<0$ の場合は,$x=1$ において $y$ が最大になることが分かるだろう。また,$a>0$ の場合は,極大で最大になるとは限らないことも分かるだろう。極大で最大となるのは,$f(4a)=f(a)$ であることを考えると,$a\leqq1\leqq4a$ すなわち $\dfrac{1}{4}\leqq a\leqq1$ のときであると分かるだろう。ここまで考えると,$\dfrac{1}{4}<a$ のときは,$x=1$ で最大となることも分かる。
したがって,$a<0$ または $\dfrac{1}{4}<a$ のとき,最大値は
\begin{align*} M(a)=f(1)=9a^2-6a+1 \end{align*}
$\dfrac{1}{4}\leqq a\leqq1$ のとき,最大値は \begin{align*} M(a)=f(a)=4a^3 \end{align*}

ヒロ
3次関数の等間隔性を知っていると,楽に感じたり,自分の計算に自身をもてるようになるだろう。
2020年 東京女子大
2020年 東京女子大$a$ を正の実数とする。3次関数 $f(x)=x^3-3a^2x$ の $-1\leqq x\leqq1$ における最大値を $m(a)$ とするとき,$m(a)$ を $a$ を用いて表せ。
【解答と考え方】
考える $x$ の範囲が $0$ に関して対称な区間であるから,3次関数のグラフの対称性に気を配ろう。一般に,3次関数のグラフは変曲点に関して点対称である。ただ,変曲点に関する知識がなくても,$f(x)=x^3-3a^2x$ を見たときに,グラフは原点に関して対称であることに気付くようにしよう。
よって,$f(x)$ の増減は次のようになる。
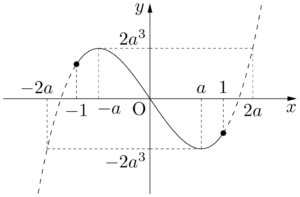
(i) $1<a$ のとき
グラフより,$m(a)=f(-1)=3a^2-1$
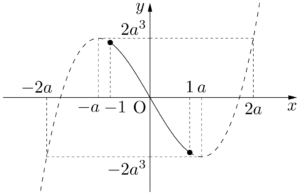
(ii) $a\leqq1<2a$ すなわち $\dfrac{1}{2}<a\leqq1$ のとき
グラフより,$m(a)=f(-a)=2a^3$
(iii) $2a\leqq1$ すなわち $0<a\leqq\dfrac{1}{2}$ のとき
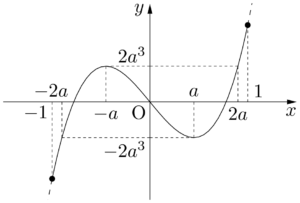
グラフより,$m(a)=f(1)=-3a^2+1$
考える $x$ の範囲が $0$ に関して対称な区間であるから,3次関数のグラフの対称性に気を配ろう。一般に,3次関数のグラフは変曲点に関して点対称である。ただ,変曲点に関する知識がなくても,$f(x)=x^3-3a^2x$ を見たときに,グラフは原点に関して対称であることに気付くようにしよう。
\begin{align*}
f(-x)&=(-x)^3-3a^2(-x) \\[4pt]
&=-x^3+3a^2x \\[4pt]
&=-f(x)
\end{align*}
が成り立つから,$f(x)$ は奇関数である。したがって,$y=f(x)$ のグラフは原点に関して対称である。f(-x)&=(-x)^3-3a^2(-x) \\[4pt]
&=-x^3+3a^2x \\[4pt]
&=-f(x)
\end{align*}
\begin{align*}
f'(x)&=3x^2-3a^2 \\[4pt]
&=3(x+a)(x-a)
\end{align*}
$f'(x)=0$ を解くと,$x=\pm a$f'(x)&=3x^2-3a^2 \\[4pt]
&=3(x+a)(x-a)
\end{align*}
よって,$f(x)$ の増減は次のようになる。
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -a & \cdots & a & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
また,$f(x)=f(-a)$ を解くと\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -a & \cdots & a & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
\begin{align*}
&x^3-3a^2x=-a^3+3a^3 \\[4pt]
&x^3-3a^2x-2a^3=0 \\[4pt]
&(x+a)^2(x-2a)=0 \\[4pt]
&x=-a,2a
\end{align*}
$a,~2a,~1$ の大小関係を考えると,3つの場合に分けることになる。&x^3-3a^2x=-a^3+3a^3 \\[4pt]
&x^3-3a^2x-2a^3=0 \\[4pt]
&(x+a)^2(x-2a)=0 \\[4pt]
&x=-a,2a
\end{align*}
(i) $1<a$ のとき

グラフより,$m(a)=f(-1)=3a^2-1$
(ii) $a\leqq1<2a$ すなわち $\dfrac{1}{2}<a\leqq1$ のとき

グラフより,$m(a)=f(-a)=2a^3$
(iii) $2a\leqq1$ すなわち $0<a\leqq\dfrac{1}{2}$ のとき

グラフより,$m(a)=f(1)=-3a^2+1$

ヒロ
3次関数の対称性については,別の記事で説明しているため,知らない人は次の記事から知識を吸収しよう。




















