ここでは2つの円の共有点を求める方法について説明します。
円と直線の共有点の座標を求める問題と比べると,大学入試で出題される頻度はかなり少ないです。
それは2つの円の共有点を求める問題が,2つの円の共有点を通る直線と2つの円の共有点を求める問題に帰着されるからでしょう。
実際の入試ではほとんど見る機会はないと思いますが,2つの円の共有点の座標を正確に求められるようにしておきましょう。
Contents
2つの円の共有点の座標を求める方法

ヒロ
2つの円が共有点をもつとき,次の3つの場合に分けられる。
- 2点で交わる
- 外接する
- 内接する

ヒロ
それぞれの場合について,2つの円の共有点の座標を求める方法を説明する。
2点で交わるとき

ヒロ
まずは2つの円が2点で交わるときの共有点の座標を求める方法を説明する。
円 $C_1:$$x^2+y^2+lx+my+n=0~\cdots\cdots①$ と円 $C_2:$$x^2+y^2+px+qy+r=0~\cdots\cdots②$ が2つの共有点P,Qをもつとする。2つの円の共有点の座標は「①かつ②」をみたす $(x,~y)$ である。
ここで,$①-②$ より
\begin{align*}
(l-p)x+(m-q)y+n-r=0~\cdots\cdots③
\end{align*}
となり,$②+③$ を計算すると①が得られるから「①かつ②」は「①かつ③」と同値である。ちなみに「2つの円の交点を通る直線」の記事で説明したように,直線③は2つの円①と②の共有点を通る直線である。(l-p)x+(m-q)y+n-r=0~\cdots\cdots③
\end{align*}
したがって,「2つの円①と②の共有点」は「円①と直線③の共有点」と一致する。あとは「円と直線の共有点」の記事でも説明したように,①と③の連立方程式を解くだけである。
ちなみに「②かつ③」としても結果は同じであるから,①と②をみて計算が楽になると思う方を使えば良い。

外接するとき

ヒロ
それでは2つの円が外接するときの共有点の座標を求める方法を説明する。
2つの円 $C_1$ と $C_2$ の半径をそれぞれ $r_1,~r_2$ とし,2つの円が点Pで外接しているときを考える。
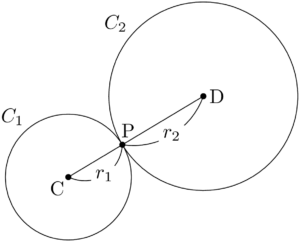
2つの円 $C_1,~C_2$ の中心をそれぞれC,Dとすると,接点Pは線分CDを $r_1:r_2$ に内分する点であることが分かる。したがって,「内分点と外分点の座標」の公式を用いることで接点Pの座標を求めることができる。
内接するとき

ヒロ
2つの円が内接するときの共有点の座標を求める方法を説明する。
2つの円 $C_1$ と $C_2$ の半径をそれぞれ $r_1,~r_2$ とし,2つの円が点Pで内接しているときを考える。
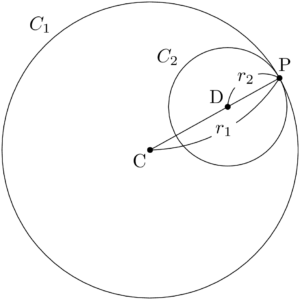
2つの円 $C_1,~C_2$ の中心をそれぞれC,Dとすると,接点Pは線分CDを $r_1:r_2$ に外分する点であることが分かる。したがって,「内分点と外分点の座標」の公式を用いることで接点Pの座標を求めることができる。



















