Contents
- ページ1
- 1 多項式の割り算とは
- ページ2
- 1 多項式の割り算
- ページ3
- 1 多項式の割り算の効率を良くしよう
- ページ4
- 1 多項式の割り算に関する問題
多項式の割り算
2020年 自治医科大整式 $4x^3-3x^2+2x-1$ を整式 $2x-1$ で割るとき,商が $ax^2+bx+c$,余りが $d$ となるとする。$a+b+c+d$ の値を求めよ。
【考え方と解答】
次のように筆算で考えよう。
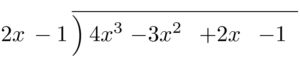
まずは $4x^3\div2x$ を計算して,商の部分に $2x^2$ と書く。
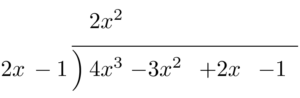
次に,$2x^2\times(2x-1)$ を計算して,割られる式の下に書いて,引き算をする。
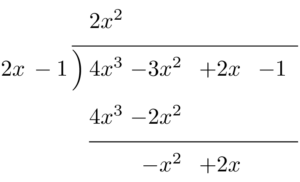
引き算で得られた式が2次式であり,割る式より次数が高いから,割り算を続ける。$-x^2\div2x$ を計算して,商の部分に $-\dfrac{1}{2}x$ を書く。
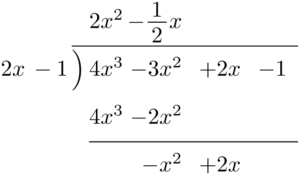
$-\dfrac{1}{2}x\times(2x-1)$ を計算して,引き算をする。
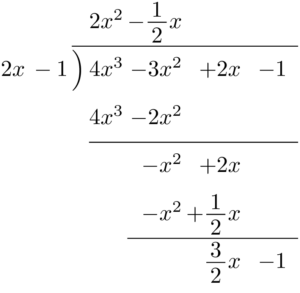
さらに続ける。 $\dfrac{3}{2}x\div2x$ を計算して,商の部分に $+\dfrac{3}{4}$ を書く。
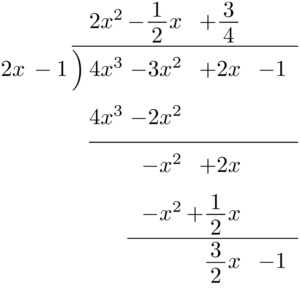
$\dfrac{3}{4}\times(2x-1)$ を計算して引き算をすると,$-\dfrac{1}{4}$ となる。
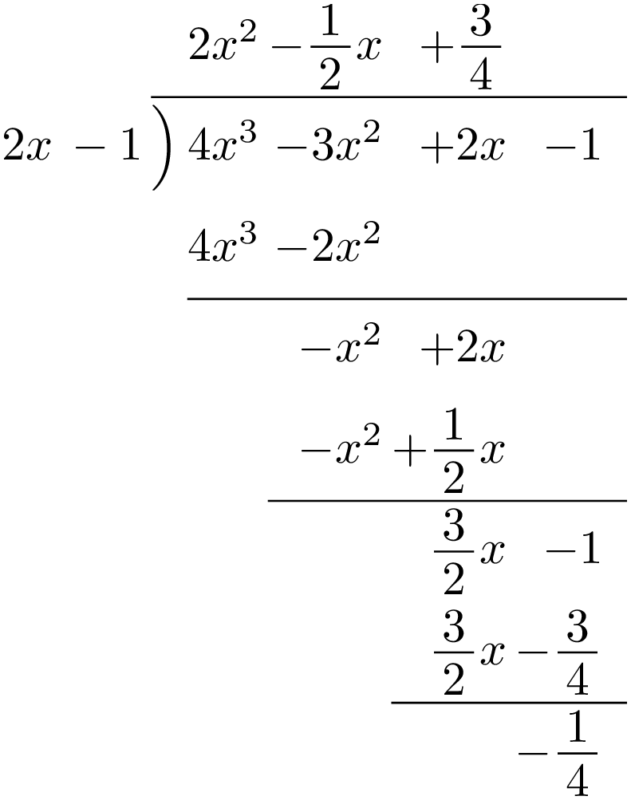
これは割る式より次数が低い定数であるから,ここで割り算が終了する。
筆算の結果より,商は $2x^2-\dfrac{1}{2}x+\dfrac{3}{4}$ であり,余りは $-\dfrac{1}{4}$ である。
よって,求める値は
次のように筆算で考えよう。
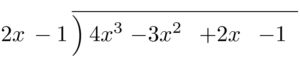
まずは $4x^3\div2x$ を計算して,商の部分に $2x^2$ と書く。
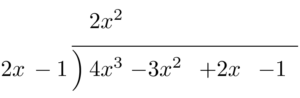
次に,$2x^2\times(2x-1)$ を計算して,割られる式の下に書いて,引き算をする。

引き算で得られた式が2次式であり,割る式より次数が高いから,割り算を続ける。$-x^2\div2x$ を計算して,商の部分に $-\dfrac{1}{2}x$ を書く。

$-\dfrac{1}{2}x\times(2x-1)$ を計算して,引き算をする。

さらに続ける。 $\dfrac{3}{2}x\div2x$ を計算して,商の部分に $+\dfrac{3}{4}$ を書く。

$\dfrac{3}{4}\times(2x-1)$ を計算して引き算をすると,$-\dfrac{1}{4}$ となる。

これは割る式より次数が低い定数であるから,ここで割り算が終了する。
筆算の結果より,商は $2x^2-\dfrac{1}{2}x+\dfrac{3}{4}$ であり,余りは $-\dfrac{1}{4}$ である。
よって,求める値は
\begin{align*}
a+b+c+d=2-\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{1}{4}=2
\end{align*}
a+b+c+d=2-\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{1}{4}=2
\end{align*}

ヒロ
割り算を真面目に行わなくても,次のように考えることで空欄を埋めることができる。
【別の考え方と解答】
割られる式,割る式,商,余りの関係より
割られる式,割る式,商,余りの関係より
\begin{align*}
4x^3-3x^2+2x-1=(2x-1)(ax^2+bx+c)+d
\end{align*}
が成り立つ。$x=1$ のとき,右辺は $a+b+c+d$ になるから,求める値は左辺に $x=1$ を代入したものである。4x^3-3x^2+2x-1=(2x-1)(ax^2+bx+c)+d
\end{align*}
\begin{align*}
a+b+c+d=4-3+2-1=2
\end{align*}
a+b+c+d=4-3+2-1=2
\end{align*}


















