Contents
3つの因数の積の形の不等式の表す領域【武蔵工業大】
2006年 武蔵工業大不等式
\begin{align*}
(x+y)(2x-y-2)(x-y+1)\leqq0
\end{align*}
の表す領域を図示せよ。(x+y)(2x-y-2)(x-y+1)\leqq0
\end{align*}
【考え方と解答】
与えられた不等式を(*)が成り立つのは,3つの因数 $x+y$,$2x-y-2$,$x-y+1$ のうち,1つまたは3つが0以下となるときである。したがって,
$①+②$ より
$m$ と $n$ の交点を求める。
$①-②$ より
$n$ と $l$ の交点を求める。
$①+③$ より
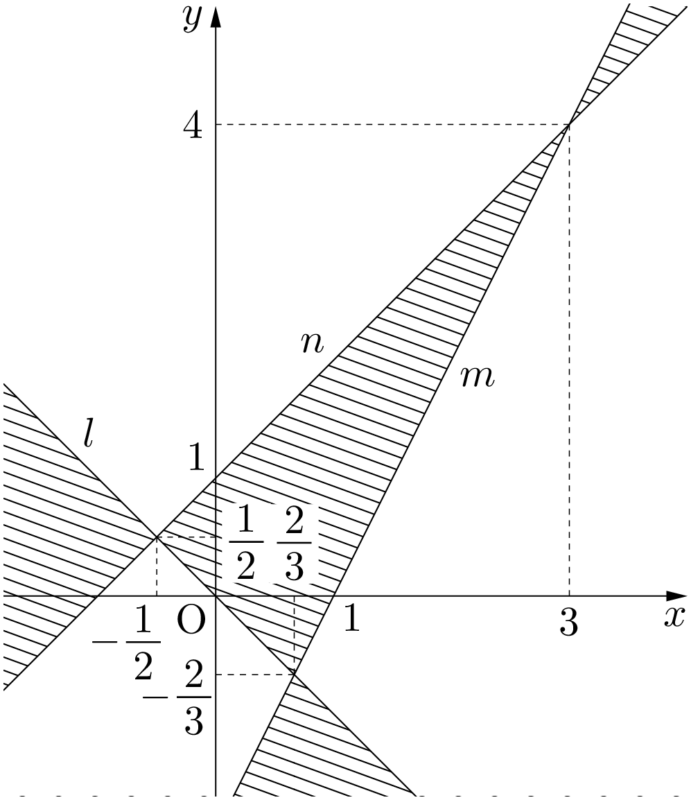
以上のことから,求める領域は下図の斜線部分(境界を含む)となる。
与えられた不等式を(*)が成り立つのは,3つの因数 $x+y$,$2x-y-2$,$x-y+1$ のうち,1つまたは3つが0以下となるときである。したがって,
\begin{align*}
&\begin{cases}
x+y\leqq0 \\[4pt]
2x-y-2\geqq0 \\[4pt]
x-y+1\geqq0
\end{cases}~または~~
\begin{cases}
x+y\geqq0 \\[4pt]
2x-y-2\leqq0 \\[4pt]
x-y+1\geqq0
\end{cases}~または\\[4pt]
&\begin{cases}
x+y\geqq0 \\[4pt]
2x-y-2\geqq0 \\[4pt]
x-y+1\leqq0
\end{cases}~または~~
\begin{cases}
x+y\leqq0 \\[4pt]
2x-y-2\leqq0 \\[4pt]
x-y+1\leqq0
\end{cases}
\end{align*}
境界線は3つの直線 $l,~m,~n$ であり,それらの方程式は次のようになる。&\begin{cases}
x+y\leqq0 \\[4pt]
2x-y-2\geqq0 \\[4pt]
x-y+1\geqq0
\end{cases}~または~~
\begin{cases}
x+y\geqq0 \\[4pt]
2x-y-2\leqq0 \\[4pt]
x-y+1\geqq0
\end{cases}~または\\[4pt]
&\begin{cases}
x+y\geqq0 \\[4pt]
2x-y-2\geqq0 \\[4pt]
x-y+1\leqq0
\end{cases}~または~~
\begin{cases}
x+y\leqq0 \\[4pt]
2x-y-2\leqq0 \\[4pt]
x-y+1\leqq0
\end{cases}
\end{align*}
\begin{align*}
&l:x+y=0 ~\cdots\cdots① \\[4pt]
&m:2x-y-2=0 ~\cdots\cdots② \\[4pt]
&n:x-y+1=0 ~\cdots\cdots③
\end{align*}
$l$ と $m$ の交点を求める。&l:x+y=0 ~\cdots\cdots① \\[4pt]
&m:2x-y-2=0 ~\cdots\cdots② \\[4pt]
&n:x-y+1=0 ~\cdots\cdots③
\end{align*}
$①+②$ より
\begin{align*}
&3x-2=0 \\[4pt]
&x=\dfrac{2}{3}
\end{align*}
よって,$l$ と $m$ は点$\left(\dfrac{2}{3},~-\dfrac{2}{3}\right)$ で交わる。&3x-2=0 \\[4pt]
&x=\dfrac{2}{3}
\end{align*}
$m$ と $n$ の交点を求める。
$①-②$ より
\begin{align*}
&x-3=0 \\[4pt]
&x=3
\end{align*}
よって,$m$ と $n$ は点 $(3,~4)$ で交わる。&x-3=0 \\[4pt]
&x=3
\end{align*}
$n$ と $l$ の交点を求める。
$①+③$ より
\begin{align*}
&2x+1=0 \\[4pt]
&x=-\dfrac{1}{2}
\end{align*}
よって,$n$ と $l$ は点 $\left(-\dfrac{1}{2},~\dfrac{1}{2}\right)$ で交わる。&2x+1=0 \\[4pt]
&x=-\dfrac{1}{2}
\end{align*}
以上のことから,求める領域は下図の斜線部分(境界を含む)となる。


ヒロ
上では丁寧に場合分けをして,求める領域に斜線を引いたが,実際にそうやっている人は少ないかもしれない。

ヒロ
領域を,もう少し楽に求める方法を知っておこう。
領域を示した図を見ると,$xy$ 平面が3直線 $l,~m,~n$ によって7つの領域に分けられていて,斜線部分と白い部分が交互になっているのが分かるだろう。動点 $(x,~y)$ が境界線を横切って隣の領域に移ると
\begin{align*}
x+y,~2x-y-2,~x-y+1
\end{align*}
のうち,ちょうど1つの符号が変わる。したがって,不等式(*)の左辺x+y,~2x-y-2,~x-y+1
\end{align*}
\begin{align*}
(x+y)(2x-y-2)(x-y+1)
\end{align*}
の符号も変わることになる。(x+y)(2x-y-2)(x-y+1)
\end{align*}

ヒロ
つまり,次の手順で条件をみたす領域を求めることができる。
不等式の表す領域の図示の仕方
- すべての境界線を図示する。
- 境界線上にない1つの点Aを決める。
- 点Aが不等式(*)をみたす場合は,その点が属する領域に斜線を引く。
- 斜線を引いた領域に隣接する領域には斜線を引かない。斜線を引かない領域に隣接する領域には斜線を引く。
※ただし,定義域に注意すること。

ヒロ
このことを考えると今回の問題では,次のように斜線を引くことができる。
【求める領域にテンポよく斜線を引く】
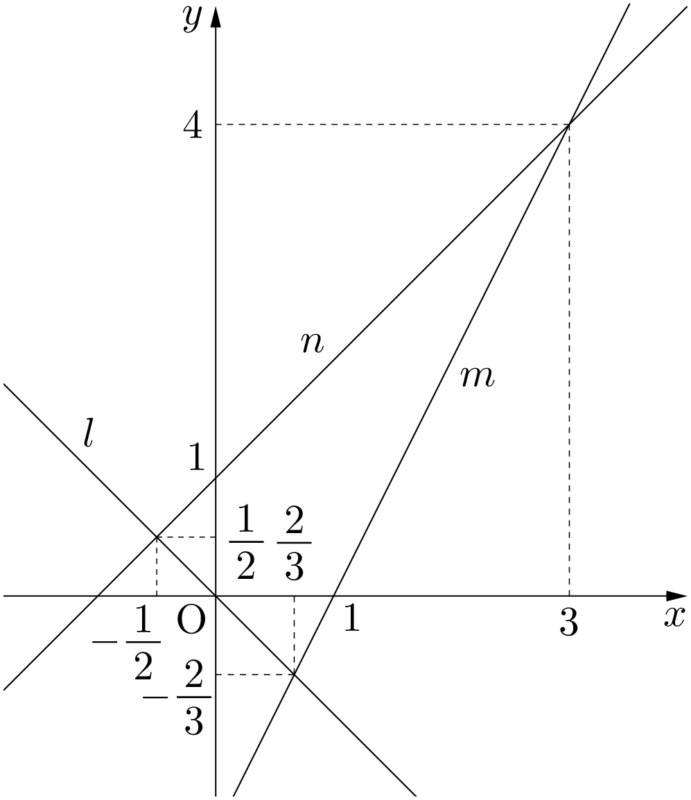
まず,境界線を引くと次のようになる。
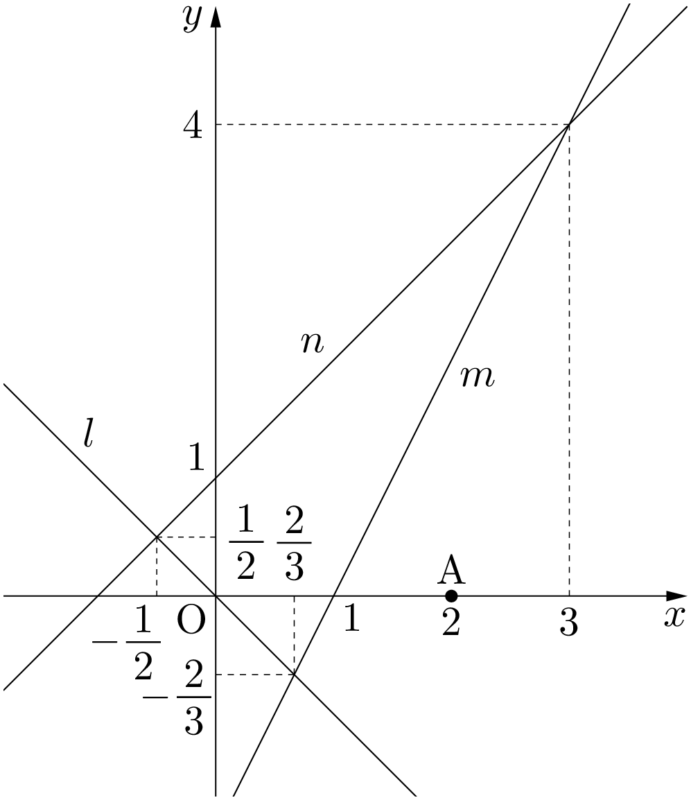
境界線上にない格子点で計算が楽な点を1つ決めよう。ここでは,例として点A$(2,~0)$ を選んでみる。
不等式(*)の左辺を $f(x,~y)$ とおくと
つまり,点Aが属する領域には斜線を引かず,その領域から境界線を1つ跨いで隣接する領域に斜線を引く。
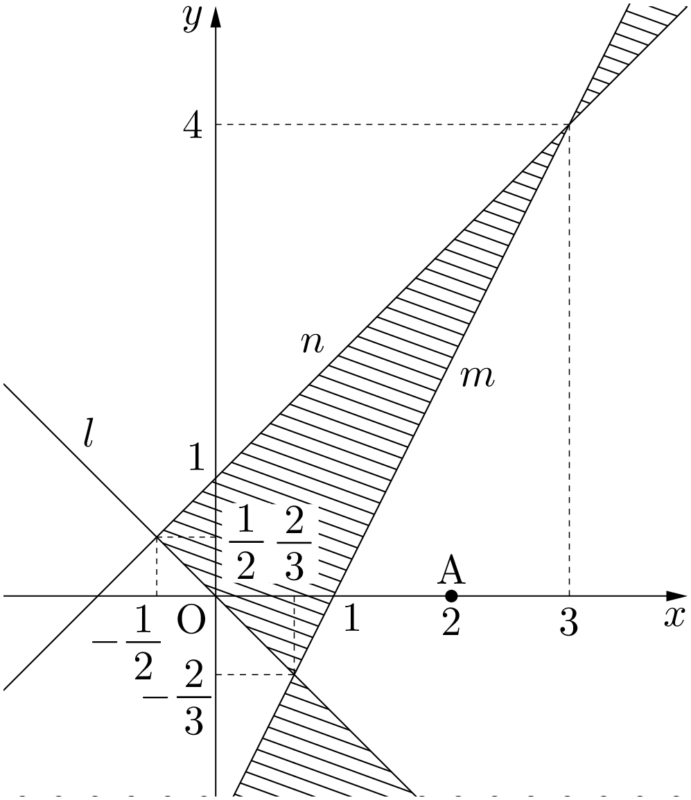
あとはこの要領で,斜線を引く領域と引かない領域が交互になるように斜線を引いていこう。この問題では,点$(-2,~0)$ が属する領域に斜線を引いて完成である。
まず,境界線を引くと次のようになる。

境界線上にない格子点で計算が楽な点を1つ決めよう。ここでは,例として点A$(2,~0)$ を選んでみる。

不等式(*)の左辺を $f(x,~y)$ とおくと
\begin{align*}
f(2,~0)&=(2+0)(4-0-2)(2-0+1) \\[4pt]
&=2\Cdota2\Cdota3=12>0
\end{align*}
となり,不等式(*)をみたさないから,点Aは求める領域の外部の点である。f(2,~0)&=(2+0)(4-0-2)(2-0+1) \\[4pt]
&=2\Cdota2\Cdota3=12>0
\end{align*}
つまり,点Aが属する領域には斜線を引かず,その領域から境界線を1つ跨いで隣接する領域に斜線を引く。

あとはこの要領で,斜線を引く領域と引かない領域が交互になるように斜線を引いていこう。この問題では,点$(-2,~0)$ が属する領域に斜線を引いて完成である。


















