Contents
積の形の不等式の表す領域【法政大】
2008年 法政大次の連立不等式の表す領域を図示せよ。
\begin{align*}
\begin{cases}
(-x^2+4x-y+2)(-x-2y+4)\leqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}
\end{align*}
\begin{cases}
(-x^2+4x-y+2)(-x-2y+4)\leqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}
\end{align*}
【考え方と解答】
与えられた不等式より
①より,$y=-\dfrac{1}{2}x+2$
①に代入すると
$C$ と $m$ の交点を求める。
③より,$y=4x-7$
①に代入すると
$l$ と $m$ の交点を求める。
$③\times2-②$ より
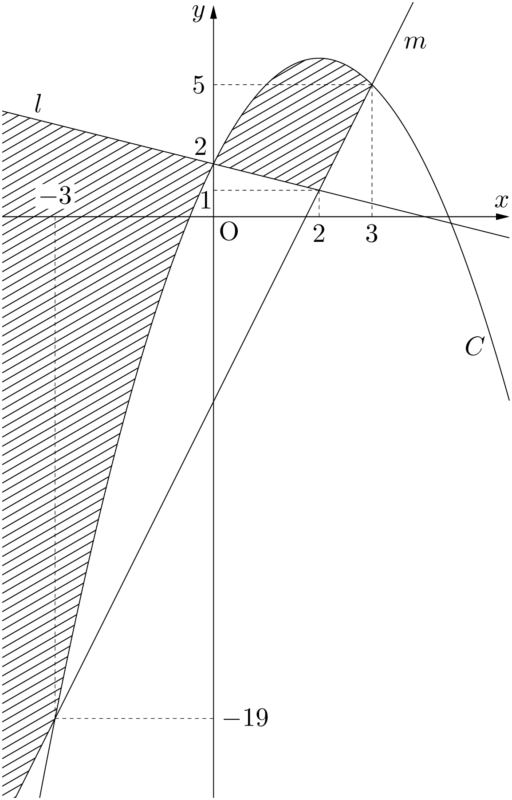
これらのことを考えると,求める領域は下図の斜線部分(境界を含む)となる。
与えられた不等式より
\begin{align*}
\begin{cases}
-x^2+4x-y+2\geqq0 \\[4pt]
-x-2y+4\leqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}~または~~
\begin{cases}
-x^2+4x-y+2\leqq0 \\[4pt]
-x-2y+4\geqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}
\end{align*}
求める領域の境界線は,放物線 $C$ と2直線 $l,~m$ でそれらの方程式はそれぞれ次のようになる。\begin{cases}
-x^2+4x-y+2\geqq0 \\[4pt]
-x-2y+4\leqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}~または~~
\begin{cases}
-x^2+4x-y+2\leqq0 \\[4pt]
-x-2y+4\geqq0 \\[4pt]
4x-y-7\leqq0
\end{cases}
\end{align*}
\begin{align*}
&C:-x^2+4x-y+2=0~\cdots\cdots① \\[4pt]
&l:-x-2y+4=0~\cdots\cdots② \\[4pt]
&m:4x-y-7=0~\cdots\cdots③
\end{align*}
$C$ と $l$ の交点を求める。&C:-x^2+4x-y+2=0~\cdots\cdots① \\[4pt]
&l:-x-2y+4=0~\cdots\cdots② \\[4pt]
&m:4x-y-7=0~\cdots\cdots③
\end{align*}
①より,$y=-\dfrac{1}{2}x+2$
①に代入すると
\begin{align*}
&-x^2+4x-\left(-\dfrac{1}{2}x+2\right)+2=0 \\[4pt]
&2x^2-9x=0 \\[4pt]
&x(2x-9)=0 \\[4pt]
&x=0,~\dfrac{9}{2}
\end{align*}
よって,$C$ と $l$ は2点 $(0,~2)$,$\left(\dfrac{9}{2},~-\dfrac{1}{4}\right)$ で交わる。&-x^2+4x-\left(-\dfrac{1}{2}x+2\right)+2=0 \\[4pt]
&2x^2-9x=0 \\[4pt]
&x(2x-9)=0 \\[4pt]
&x=0,~\dfrac{9}{2}
\end{align*}
$C$ と $m$ の交点を求める。
③より,$y=4x-7$
①に代入すると
\begin{align*}
&-x^2+4x-(4x-7)+2=0 \\[4pt]
&x^2=9 \\[4pt]
&x=\pm3
\end{align*}
よって,$C$ と $m$ は2点 $(-3,~-19)$,$(3,~5)$ で交わる。&-x^2+4x-(4x-7)+2=0 \\[4pt]
&x^2=9 \\[4pt]
&x=\pm3
\end{align*}
$l$ と $m$ の交点を求める。
$③\times2-②$ より
\begin{align*}
&9x-18=0 \\[4pt]
&x=2
\end{align*}
よって,$l$ と $m$ は点 $(2,~1)$ で交わる。&9x-18=0 \\[4pt]
&x=2
\end{align*}
これらのことを考えると,求める領域は下図の斜線部分(境界を含む)となる。

2つの因数の積の形の不等式の表す領域【武蔵工業大】
2005年 武蔵工業大不等式
\begin{align*}
(x^2+y^2-2)(x^2+y^2-4x+2)\leqq0
\end{align*}
で表される領域の面積を求めよ。(x^2+y^2-2)(x^2+y^2-4x+2)\leqq0
\end{align*}
【考え方と解答】
与えられた不等式より
2つの円の共有点を求める。$①-②$ より
以上より,与えられた不等式が表す領域は下図の斜線部分(境界を含む)である。
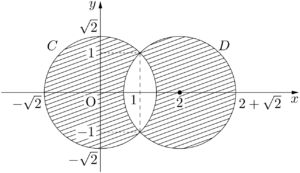
斜線部分の面積を求めるために,補助線を引く。2つの円の交点をP,Qとする。
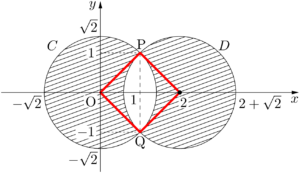
赤い補助線の四角形は一辺の長さが $\sqrt{2}$ の正方形である。円 $C$ の弧 $\ko{\textrm{PQ}}$ と弦PQで囲まれた部分の面積は
与えられた不等式より
\begin{align*}
\begin{cases}
x^2+y^2-2\geqq0 \\[4pt]
x^2+y^2-4x+2\leqq0
\end{cases}~または~~
\begin{cases}
x^2+y^2-2\leqq0 \\[4pt]
x^2+y^2-4x+2\geqq0
\end{cases}
\end{align*}
領域の境界は2つの円 $C,~D$ であり,それらの方程式は次のようになる。\begin{cases}
x^2+y^2-2\geqq0 \\[4pt]
x^2+y^2-4x+2\leqq0
\end{cases}~または~~
\begin{cases}
x^2+y^2-2\leqq0 \\[4pt]
x^2+y^2-4x+2\geqq0
\end{cases}
\end{align*}
\begin{align*}
&C:x^2+y^2=2~\cdots\cdots① \\[4pt]
&D:x^2+y^2-4x+2=0~\cdots\cdots②
\end{align*}
円 $C$ は原点を中心とする半径 $\sqrt{2}$ の円である。②を変形すると&C:x^2+y^2=2~\cdots\cdots① \\[4pt]
&D:x^2+y^2-4x+2=0~\cdots\cdots②
\end{align*}
\begin{align*}
(x-2)^2+y^2=2
\end{align*}
となるから,円 $D$ は点 $(2,~0)$ を中心とする半径 $\sqrt{2}$ の円である。(x-2)^2+y^2=2
\end{align*}
2つの円の共有点を求める。$①-②$ より
\begin{align*}
&4x=4 \\[4pt]
&x=1
\end{align*}
よって,2つの円 $C,~D$ は2点 $(1,~1)$,$(1,~-1)$ で交わる。&4x=4 \\[4pt]
&x=1
\end{align*}
以上より,与えられた不等式が表す領域は下図の斜線部分(境界を含む)である。

斜線部分の面積を求めるために,補助線を引く。2つの円の交点をP,Qとする。

赤い補助線の四角形は一辺の長さが $\sqrt{2}$ の正方形である。円 $C$ の弧 $\ko{\textrm{PQ}}$ と弦PQで囲まれた部分の面積は
\begin{align*}
&(扇形\text{OPQ})-\sankaku{OPQ} \\[4pt]
&=\dfrac{1}{4}(\sqrt{2})^2\pi-\dfrac{1}{2}(\sqrt{2})^2 \\[4pt]
&=\dfrac{\pi}{2}-1
\end{align*}
したがって,求める斜線部分の面積は&(扇形\text{OPQ})-\sankaku{OPQ} \\[4pt]
&=\dfrac{1}{4}(\sqrt{2})^2\pi-\dfrac{1}{2}(\sqrt{2})^2 \\[4pt]
&=\dfrac{\pi}{2}-1
\end{align*}
\begin{align*}
2\left\{\pi(\sqrt{2})^2-2\left(\dfrac{\pi}{2}-1\right)\right\}=2\pi+4
\end{align*}
2\left\{\pi(\sqrt{2})^2-2\left(\dfrac{\pi}{2}-1\right)\right\}=2\pi+4
\end{align*}


















