Contents
- ページ1
- 1 2020年 愛知学院大
- ページ2
- 1 2018年 自治医科大
- ページ3
- 1 2018年 東京理科大
2018年 東京理科大
2018年 東京理科大$f(x)=\dfrac{\sin x+\sqrt{3}\cos x+1}{2\sin x+2\sqrt{3}\cos x+6}$ $(0\leqq x<2\pi)$ とおく。
(1) $f(\pi)=-\dfrac{\sqrt{\myhako}}{\myhako}$ である。また,$f(x)=f(\pi)$ となる $\pi$ 以外の $x$ の値は $x=\dfrac{\myhako}{\myhako}\pi$ である。
(2) $f(x)=0$ となる $x$ は,小さいものから順に,$x=\dfrac{\myhako}{\myhako}\pi$,$x=\dfrac{\myhako}{\myhako}\pi$ である。
(3) $f(x)$ は,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最大値 $\dfrac{\myhako}{\myhako}$ をとり,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最小値 $-\dfrac{\myhako}{\myhako}\pi$ をとる。
(1) $f(\pi)=-\dfrac{\sqrt{\myhako}}{\myhako}$ である。また,$f(x)=f(\pi)$ となる $\pi$ 以外の $x$ の値は $x=\dfrac{\myhako}{\myhako}\pi$ である。
(2) $f(x)=0$ となる $x$ は,小さいものから順に,$x=\dfrac{\myhako}{\myhako}\pi$,$x=\dfrac{\myhako}{\myhako}\pi$ である。
(3) $f(x)$ は,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最大値 $\dfrac{\myhako}{\myhako}$ をとり,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最小値 $-\dfrac{\myhako}{\myhako}\pi$ をとる。

ヒロ
三角関数の分数式を見たときには,「図形的処理ができるかどうか」を考えるようにしよう。

ヒロ
そのためには,次の記事で説明している2つ目の考え方が参考になるだろう。
【(1)の考え方と解答】
$x=\pi$ を代入して値を求めよう。
$x=\pi$ を代入して値を求めよう。
\begin{align*}
f(\pi)&=\dfrac{\sin\pi+\sqrt{3}\cos\pi+1}{2\sin\pi+2\sqrt{3}\cos\pi+6} \\[4pt]
&=\dfrac{-\sqrt{3}+1}{-2\sqrt{3}+6}=\dfrac{-\sqrt{3}+1}{-2\sqrt{3}(1-\sqrt{3})} \\[4pt]
&=-\dfrac{\sqrt{3}}{6}
\end{align*}
f(\pi)&=\dfrac{\sin\pi+\sqrt{3}\cos\pi+1}{2\sin\pi+2\sqrt{3}\cos\pi+6} \\[4pt]
&=\dfrac{-\sqrt{3}+1}{-2\sqrt{3}+6}=\dfrac{-\sqrt{3}+1}{-2\sqrt{3}(1-\sqrt{3})} \\[4pt]
&=-\dfrac{\sqrt{3}}{6}
\end{align*}

ヒロ
この問題では,約分することで分母の有理化をしている。

ヒロ
後半の問題は,$\sin x,~\cos x$ の定義を利用して解くことにする。
【(1)の後半の考え方と解答】
$\cos x=X,~\sin x=Y$ とおくと,
$X=-\dfrac{1}{2}$ のとき,$Y=-\dfrac{\sqrt{3}}{2}$
計算して求めたが,直線②が点C$(-1,~0)$ を通ることを考えて図を描いてサクッと求めても良いだろう。
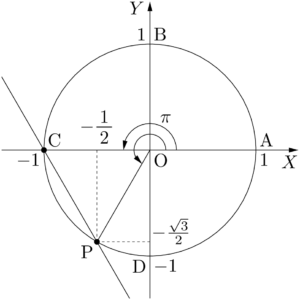
$x$ の値が $\pi$ 以外になるのは,上図の点Pのときだから,$x=\dfrac{4}{3}\pi$ である。
$\cos x=X,~\sin x=Y$ とおくと,
\begin{align*}
X^2+Y^2=1~\cdots\cdots①
\end{align*}
が成り立つ。$f(x)=f(\pi)$ よりX^2+Y^2=1~\cdots\cdots①
\end{align*}
\begin{align*}
&\dfrac{Y+\sqrt{3}X+1}{2Y+2\sqrt{3}X+6}=-\dfrac{1}{2\sqrt{3}} \\[4pt]
&\sqrt{3}(Y+\sqrt{3}X+1)+(Y+\sqrt{3}X+3)=0 \\[4pt]
&\sqrt{3}(\sqrt{3}+1)X+(\sqrt{3}+1)Y+\sqrt{3}(1+\sqrt{3})=0 \\[4pt]
&\sqrt{3}X+Y+\sqrt{3}=0 \\[4pt]
&Y=-\sqrt{3}(X+1)~\cdots\cdots②
\end{align*}
②を①に代入すると&\dfrac{Y+\sqrt{3}X+1}{2Y+2\sqrt{3}X+6}=-\dfrac{1}{2\sqrt{3}} \\[4pt]
&\sqrt{3}(Y+\sqrt{3}X+1)+(Y+\sqrt{3}X+3)=0 \\[4pt]
&\sqrt{3}(\sqrt{3}+1)X+(\sqrt{3}+1)Y+\sqrt{3}(1+\sqrt{3})=0 \\[4pt]
&\sqrt{3}X+Y+\sqrt{3}=0 \\[4pt]
&Y=-\sqrt{3}(X+1)~\cdots\cdots②
\end{align*}
\begin{align*}
&X^2+3(X+1)^2=1 \\[4pt]
&4X^2+6X+2=0 \\[4pt]
&2X^2+3X+1=0 \\[4pt]
&(X+1)(2X+1)=0 \\[4pt]
&X=-1,~-\dfrac{1}{2}
\end{align*}
$X=-1$ のとき,$Y=0$&X^2+3(X+1)^2=1 \\[4pt]
&4X^2+6X+2=0 \\[4pt]
&2X^2+3X+1=0 \\[4pt]
&(X+1)(2X+1)=0 \\[4pt]
&X=-1,~-\dfrac{1}{2}
\end{align*}
$X=-\dfrac{1}{2}$ のとき,$Y=-\dfrac{\sqrt{3}}{2}$
計算して求めたが,直線②が点C$(-1,~0)$ を通ることを考えて図を描いてサクッと求めても良いだろう。

$x$ の値が $\pi$ 以外になるのは,上図の点Pのときだから,$x=\dfrac{4}{3}\pi$ である。
(2) $f(x)=0$ となる $x$ は,小さいものから順に,$x=\dfrac{\myhako}{\myhako}\pi$,$x=\dfrac{\myhako}{\myhako}\pi$ である。
【(2)の考え方と解答】
(1)と同じように,$\cos x=X,~\sin x=Y$ とおいて考える。$f(x)=0$ のとき
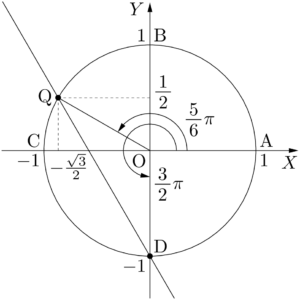
よって,$f(x)=0$ となる $x$ は小さいものから順に,$x=\dfrac{5}{6}\pi$,$x=\dfrac{3}{2}\pi$ である。
(1)と同じように,$\cos x=X,~\sin x=Y$ とおいて考える。$f(x)=0$ のとき
\begin{align*}
Y+\sqrt{3}X+1=0
\end{align*}
下図のように図を描いて単位円との交点を求めると,点Q$\left(-\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}\right)$ と点D$(0,~-1)$ が得られる。Y+\sqrt{3}X+1=0
\end{align*}

よって,$f(x)=0$ となる $x$ は小さいものから順に,$x=\dfrac{5}{6}\pi$,$x=\dfrac{3}{2}\pi$ である。
(3) $f(x)$ は,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最大値 $\dfrac{\myhako}{\myhako}$ をとり,$x=\dfrac{\myhako}{\myhako}\pi$ のとき最小値 $-\dfrac{\myhako}{\myhako}\pi$ をとる。
【(3)の考え方と解答】
(1),(2)を解いた後だと,$f(x)=(定数)$ は右辺の定数の値にかかわらず,傾きが $-\sqrt{3}$ の直線を表すのではないかと予想できる。$f(x)=k$ とおいて変形してみよう。
直線③が単位円と接するとき,接点は直線 $Y=\dfrac{1}{\sqrt{3}}X$ と単位円の交点であり,2点R$\left(\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}\right)$,S$\left(-\dfrac{\sqrt{3}}{2},~-\dfrac{1}{2}\right)$ である。
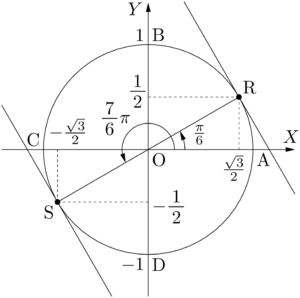
直線③が点Rを通るとき,切片 $m$ が最大になり,$k$ も最大となる。このとき $x=\dfrac{\pi}{6}$ で,最大値は
(1),(2)を解いた後だと,$f(x)=(定数)$ は右辺の定数の値にかかわらず,傾きが $-\sqrt{3}$ の直線を表すのではないかと予想できる。$f(x)=k$ とおいて変形してみよう。
\begin{align*}
&\dfrac{Y+\sqrt{3}X+1}{2Y+2\sqrt{3}X+6}=k \\[4pt]
&Y+\sqrt{3}X+1=k(2Y+2\sqrt{3}X+6) \\[4pt]
&(2k-1)\sqrt{3}X+(2k-1)Y+6k-1=0
\end{align*}
ここで,$k=\dfrac{1}{2}$ のときは上の等式が成り立たないから,$k=\dfrac{1}{2}$ となることはない。したがって,両辺を $2k-1$ で割ると&\dfrac{Y+\sqrt{3}X+1}{2Y+2\sqrt{3}X+6}=k \\[4pt]
&Y+\sqrt{3}X+1=k(2Y+2\sqrt{3}X+6) \\[4pt]
&(2k-1)\sqrt{3}X+(2k-1)Y+6k-1=0
\end{align*}
\begin{align*}
\sqrt{3}X+Y+\dfrac{6k-1}{2k-1}=0
\end{align*}
となる。$\dfrac{6k-1}{2k-1}=-m$ とおくと\sqrt{3}X+Y+\dfrac{6k-1}{2k-1}=0
\end{align*}
\begin{align*}
Y=-\sqrt{3}X+m~\cdots\cdots③
\end{align*}
となり,これは傾きが $-\sqrt{3}$,切片が $m$ の直線を表す。ここでY=-\sqrt{3}X+m~\cdots\cdots③
\end{align*}
\begin{align*}
m&=-3-\dfrac{2}{2k-1}
\end{align*}
となるから,$k$ が大きくなると $m$ も大きくなり,$k$ が小さくなると $m$ も小さくなることが分かる。つまり,$k$ の最大最小と切片 $m$ の最大最小がそのまま対応することになる。m&=-3-\dfrac{2}{2k-1}
\end{align*}
直線③が単位円と接するとき,接点は直線 $Y=\dfrac{1}{\sqrt{3}}X$ と単位円の交点であり,2点R$\left(\dfrac{\sqrt{3}}{2},~\dfrac{1}{2}\right)$,S$\left(-\dfrac{\sqrt{3}}{2},~-\dfrac{1}{2}\right)$ である。

直線③が点Rを通るとき,切片 $m$ が最大になり,$k$ も最大となる。このとき $x=\dfrac{\pi}{6}$ で,最大値は
\begin{align*}
f\left(\dfrac{\pi}{6}\right)&=\dfrac{\sin\dfrac{\pi}{6}+\sqrt{3}\cos\dfrac{\pi}{6}+1}{2\sin\dfrac{\pi}{6}+2\sqrt{3}\cos\dfrac{\pi}{6}+6} \\[4pt]
&=\dfrac{\dfrac{1}{2}+\dfrac{3}{2}+1}{1+3+6}=\dfrac{3}{10}
\end{align*}
直線③が点Sを通るとき,切片 $m$ が最小になり,$k$ も最小になる。このとき $x=\dfrac{7}{6}\pi$ で,最小値はf\left(\dfrac{\pi}{6}\right)&=\dfrac{\sin\dfrac{\pi}{6}+\sqrt{3}\cos\dfrac{\pi}{6}+1}{2\sin\dfrac{\pi}{6}+2\sqrt{3}\cos\dfrac{\pi}{6}+6} \\[4pt]
&=\dfrac{\dfrac{1}{2}+\dfrac{3}{2}+1}{1+3+6}=\dfrac{3}{10}
\end{align*}
\begin{align*}
f\left(\dfrac{7}{6}\pi\right)&=\dfrac{\sin\dfrac{7}{6}\pi+\sqrt{3}\cos\dfrac{7}{6}\pi+1}{2\sin\dfrac{7}{6}\pi+2\sqrt{3}\cos\dfrac{7}{6}\pi+6} \\[4pt]
&=\dfrac{-\dfrac{1}{2}-\dfrac{3}{2}+1}{-1-3+6}=-\dfrac{1}{2}
\end{align*}
f\left(\dfrac{7}{6}\pi\right)&=\dfrac{\sin\dfrac{7}{6}\pi+\sqrt{3}\cos\dfrac{7}{6}\pi+1}{2\sin\dfrac{7}{6}\pi+2\sqrt{3}\cos\dfrac{7}{6}\pi+6} \\[4pt]
&=\dfrac{-\dfrac{1}{2}-\dfrac{3}{2}+1}{-1-3+6}=-\dfrac{1}{2}
\end{align*}



















