Contents
直径の両端が与えられた円の方程式の導出
問題2点A$(a,~b)$,B$(c,~d)$ を直径の両端とする円の方程式を求めよ。

ヒロ
2つの方法で直径の両端が与えられた円の方程式を導出する。
円の中心と半径を求める

ヒロ
今更であるが,直径の説明をしておく。
直径とは円周上の2点を結ぶ線分(弦という)の中で,円の中心を通るものやその長さのことである。
【考え方と解答】
直径ABの中点が円の中心Cであるから,Cの座標は $\left(\dfrac{a+c}{2},~\dfrac{b+d}{2}\right)$ である。半径を $r$ とすると
直径ABの中点が円の中心Cであるから,Cの座標は $\left(\dfrac{a+c}{2},~\dfrac{b+d}{2}\right)$ である。半径を $r$ とすると
\begin{align*}
r^2&=\text{AC}^2 \\[4pt]
&=\left(a-\dfrac{a+c}{2}\right)^2+\left(b-\dfrac{b+d}{2}\right)^2 \\[4pt]
&=\left(\dfrac{a-c}{2}\right)^2+\left(\dfrac{b-d}{2}\right)^2 \\[4pt]
&=\dfrac{(a-c)^2+(b-d)^2}{4}
\end{align*}
よって,求める円の方程式はr^2&=\text{AC}^2 \\[4pt]
&=\left(a-\dfrac{a+c}{2}\right)^2+\left(b-\dfrac{b+d}{2}\right)^2 \\[4pt]
&=\left(\dfrac{a-c}{2}\right)^2+\left(\dfrac{b-d}{2}\right)^2 \\[4pt]
&=\dfrac{(a-c)^2+(b-d)^2}{4}
\end{align*}
\begin{align*}
\left(x-\dfrac{a+c}{2}\right)^2+\left(y-\dfrac{b+d}{2}\right)^2=\dfrac{(a-c)^2+(b-d)^2}{4}
\end{align*}
\left(x-\dfrac{a+c}{2}\right)^2+\left(y-\dfrac{b+d}{2}\right)^2=\dfrac{(a-c)^2+(b-d)^2}{4}
\end{align*}

ヒロ
$\text{AC}^2$ を計算して $r^2$ を求めたが,$\text{BC}^2$ を計算しても同じ結果になる。
直径を斜辺とする直角三角形に着目する

ヒロ
直径に対する円周角が $90\Deg$ であることを利用して円の方程式を導こう。
2点A$(a,~b)$,B$(c,~d)$ を直径の両端とする円の方程式を求めよ。
【考え方と解答】
ABが直径であるから,円周上の点をP$(x,~y)$ とすると,点Pが2点A,Bと一致しないときは $\kaku{APB}=90\Deg$ である。
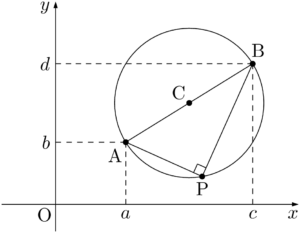
APとBPの傾きの積が $-1$ であるから
ABが直径であるから,円周上の点をP$(x,~y)$ とすると,点Pが2点A,Bと一致しないときは $\kaku{APB}=90\Deg$ である。

APとBPの傾きの積が $-1$ であるから
\begin{align*}
&\dfrac{y-b}{x-a}\Cdota\dfrac{y-d}{x-c}=-1~\cdots\cdots① \\[4pt]
&(x-a)(x-c)+(y-b)(y-d)=0~\cdots\cdots②
\end{align*}
&\dfrac{y-b}{x-a}\Cdota\dfrac{y-d}{x-c}=-1~\cdots\cdots① \\[4pt]
&(x-a)(x-c)+(y-b)(y-d)=0~\cdots\cdots②
\end{align*}

ヒロ
この書き方では,傾きが定義されない点Pを除く必要があり,そのことに触れていないと減点される可能性がある。
【傾きが定義されない点は4か所ある】
APやBPの傾きが定義されないのは,次の2つの場合がある。
- 点Pが点Aや点Bと一致するとき
- APやBPが座標軸と平行になるとき
すなわち,点Pが次のA,B,P$_1$,P$_2$ の4点と一致するときである。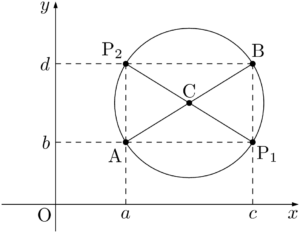
傾きの積が $-1$ になることを利用して解答を書く場合は,上図の4点を除いた状態で考えていることに触れておこう。その後,除いた4点が求めた円周上の点であることを記述しよう。それは面倒だと感じる場合は,「傾きの積が $-1$」である式①を省略して,式②から書けば良い。式②の前に何らかの説明を書き加えたいなら,ベクトルで考えていることを書くと良いだろう。

ヒロ
ベクトルで考えたときの記述については,次の記事が参考になるだろう。



















