直線や曲線が通過する領域を図示する問題って難しく感じて,見た瞬間諦めていませんか?領域は点の集まりであるから,直線や曲線がどんな点を通るかを考えれば良いということを理解しましょう。
また,包絡線について知ることで,直線の通過領域を求める問題を楽に速く解けるようにしましょう。
この記事を読むことで,包絡線に関する知識を用いて,次の問題を楽に解けるようになります。
Contents
直線が通過する点とは?

求めるのは直線が通過する領域だけど,そもそも領域は点の集まりだと考えよう。つまり,まずは具体的にどんな点を通るのかを考えてみよう。
(1) 点A $(2,-1)$
(2) 点B $(-2,4)$
(3) 点C $(-1,3)$

直線が与えられた点を通るかどうかって,代入して成り立つかどうかってことですよね?

そうだね。

(1)の場合は, $\ell$ の式に $(x,y)=(2,-1)$ を代入して $t$ の値を調べます。
&-1=2t\Cdota2-t^2 \\[4pt]
&t^2-4t-1=0 \\[4pt]
&t=2\pm\sqrt{5}
\end{align*}

$t=2\pm\sqrt{5}$ のときに,直線 $\ell$ は点Aを通ります。

$t$ が2つあるのにはどんな意味があるか分かる?

$t=2+\sqrt{5}$ のときと $t=2-\sqrt{5}$ のときに点Aを通るってことですよね。$t$ が違えば直線も異なるので,直線が2本あるってことですね。

その通り!$t$ の個数と直線の本数が一致していると分かることも重要だね。じゃあ,残りの(2),(3)もやってみてくれる?

任せて下さい。
&4=-4t-t^2 \\[4pt]
&t^2+4t+4=0 \\[4pt]
&(t+2)^2=0 \\[4pt]
&t=-2
\end{align*}

$t=-2$ のときに点Bを通ります。
&3=-2t-t^2 \\[4pt]
&t^2+2t+3=0 \\[4pt]
&t=-1\pm\sqrt{2}i
\end{align*}

$t$ が複素数になったので,直線 $\ell$ は点Cを通りません。

これは簡単すぎたか。直線 $\ell$ がある点を通るかどうかは,その点の座標を代入して,その方程式を満たす実数 $t$ が存在するかどうかを調べれば良いってことだね。
直線 $y=2tx-t^2$ が通過する領域を解の配置問題として解く方法

ということは,解の配置問題に置き換えて考えれば良いね。
&Y=2tX-t^2 \\[4pt]
&t^2-2Xt+Y=0~\cdots\cdots ①
\end{align*}
(i) $X<-1$のとき
条件を満たすのは $f(-1)\leqq0$ かつ $f(2)\geqq0$ となるときだから,
&\begin{cases}
1+2X+Y\leqq0 \\[4pt]
4-4X+Y\geqq0
\end{cases}\\[4pt]
&\begin{cases}
y\leqq-2X-1 \\[4pt]
y\geqq4X-4
\end{cases}
\end{align*}
条件を満たすのは $D\geqq0$ かつ「$f(-1)\geqq0$ または $f(2)\geqq0$」となるときだから,
&X^2-Y\geqq0~~かつ~~「1+2X+Y\geqq0~または~4-4X+Y\geqq0」 \\[4pt]
&\begin{cases}
Y\leqq X^2 \\[4pt]
Y\geqq-2X-1~または~Y\geqq4X-4
\end{cases}
\end{align*}
条件を満たすのは $f(-1)\geqq0$ かつ $f(2)\leqq0$ となるときだから,
&\begin{cases}
1+2X+Y\geqq0 \\[4pt]
4-4X+Y\leqq0
\end{cases}\\[4pt]
&\begin{cases}
Y\geqq-2X-1 \\[4pt]
Y\leqq4X-4
\end{cases}
\end{align*}
ただし,境界を含む。
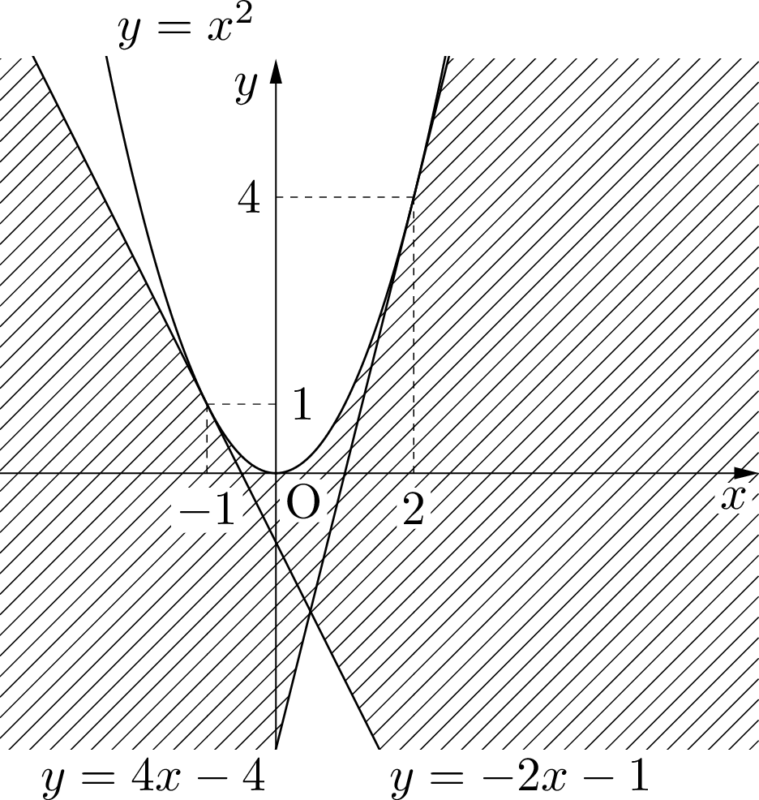
包絡線が放物線になる直線の通過領域

ここで,もう1問解いてもらおう。
(1) 点 $(t,t^2)$ における接線を $\ell$ とするとき,直線 $\ell$ の方程式を求めよ。
(2) 実数 $t$ が $-1\leqq t\leqq2$ で変化するとき,接点と接線がどのように変化していくかに着目し,直線 $\ell$ が通りうる範囲が前問と同じになることを確認せよ。

問題1と何か関連があると信じて解きますよ?
&y=2t(x-t)+t^2 \\[4pt]
&y=2tx-t^2
\end{align*}

え・・?この直線は問題1と同じなんですね。

そうだね。ってことは (2) はもう分かるね?

実際に直線が動く様子を確認しよう!
※緑の点が接点を示しています。
※geogebra の埋め込みのコードを張り付けてますが,スマホで見た場合,下に大きな空白が発生してしまいます。余分な空白が出ない方法を知ってる方がいらっしゃいましたら,コッソリ教えて下さい。

この問題では,直線 $\ell$ の包絡線が放物線 $y=x^2$ だということになるね。

なるほど。確かに直線 $\ell$ が放物線 $y=x^2$ に接しながら動きますね。

問題1を解くときに,直線 $\ell$ の包絡線が放物線 $y=x^2$ になることが最初に分かれば楽だよね。

いまは言われたから分かったわけで,それが簡単に分かれば苦労しませんね・・・
包絡線を求めて直線の通過領域を図示する方法

入試問題で直線が動くときは,ある曲線に接しながら動いていると考えよう。直線がランダムに動いて,その領域を図示するような問題が出るわけないよね。
パラメータ $t$ の値に関係なく,直線 $\ell$ に常に接する曲線のことを,直線 $\ell$ の包絡線という。直線 $\ell$ の方程式を $t$ の2次方程式とみることができるときは,判別式を $D$ とすると,包絡線の方程式は,$D=0$ で表される。
一般に,直線や曲線 $C$ の方程式が $f(x,~y,~t)=0$ 表されるときは,
\begin{cases}
f(x,~y,~t)=0 \\[4pt]
\dfrac{\partial}{\partial t}f(x,~y,~t)=0
\end{cases}
\end{align*}

確かに問題1を解いたときの $D=0$ が $y=x^2$ になってますね。

ということで,次のように解答の下準備を進めていこう。
$(判別式)=0$ より,
&x^2-y=0 \\[4pt]
&y=x^2
\end{align*}
次に接点を求める。微分すると,$y’=2x$ となり,傾きは $2t$ だから等号で結んで
&2x=2t \\[4pt]
&x=t
\end{align*}

実際に解答を書くときは次のように書こう。
&y=2t(x-t)+t^2 \\[4pt]
&y=2tx-t^2
\end{align*}
$-1\leqq t\leqq2$ のとき,接点は放物線 $y=x^2$ 上を $(-1,1)$ から $(2,4)$ まで動く。
よって,求める領域は図の斜線部分となる。ただし,境界を含む。

入試問題

じゃあ,練習しておこうか。

やっぱり少し捻ってきましたね・・・
これを $t$ の2次方程式とみると,$2t^2-xt+y-1=0$ で $(判別式)=0$ を考えると
&x^2-8(y+1)=0 \\[4pt]
&y=\dfrac{1}{8}x^2+1
\end{align*}

これで,直線の正体は分かりましたよ!
$y=(\cos\theta)x+\cos2\theta$より,$y=tx+2t^2-1~\cdot\cdots$ ①
ここで,$f(x)=-\dfrac{1}{8}x^2-1$ とおくと,$f'(x)=-\dfrac{1}{4}x$ だから,$y=f(x)$ 上の点 $(-4t,-2t^2-1)$ における接線は
&y=t(x+4t)-2t^2-1 \\[4pt]
&y=tx+2t^2-1
\end{align*}
$-1\leqq t\leqq1$ のとき,接点は $y=f(x)$ 上の $-4\leqq x\leqq4$ の部分を動くから,求める領域は図の斜線部分となる。ただし,境界を含む。


簡単に解けますね!
入試問題2

直線の方程式を $t$ の3次方程式とみて,直線の包絡線の方程式を求めよう。
2t^3-3xt^2+3x+y=0
\end{align*}
&6t^2-6xt=0 \\[4pt]
&t(t-x)=0 \\[4pt]
&t=0,~x
\end{align*}
&y=3(x^2-1)x-2x^3 \\[4pt]
&y=x^3-3x
\end{align*}

これで,与えられた直線の包絡線が $y=x^3-3x$ だと分かったね。
$f(x)=x^3-3x$ とすると
f'(x)=3x^2-3
\end{align*}
&y=(3t^2-3)(x-t)+t^3-3t \\[4pt]
&y=3(t^2-1)x-2t^3
\end{align*}
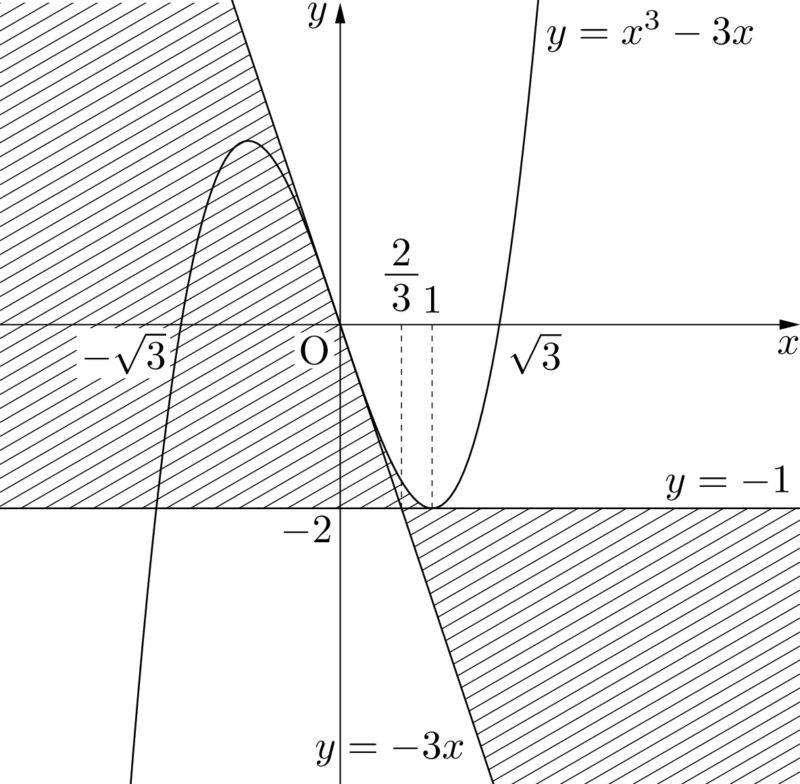
まとめ

包絡線を利用する解法を身に付けることで,楽に速く解答を書くことができる。


















