方程式の整数解 －不定方程式－【昭和女子大・立命館大】

Contents

不定方程式の問題【昭和女子大】

2020年昭和女子大方程式 $7x-5y=3~\cdots\cdots(*)$ の自然数の解 $(x,~y)$ を考える。
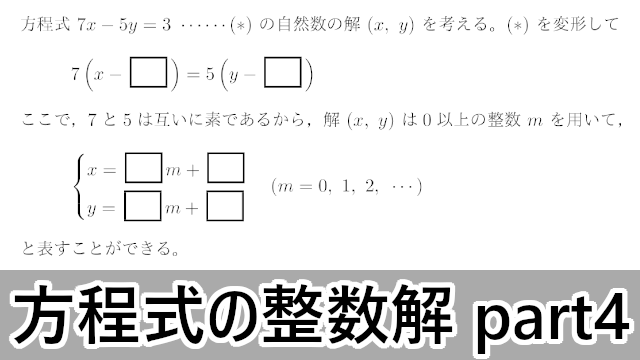
(1) $(*)$ を変形して

\begin{align*}
7\left(x-\myhako\right)=5\left(y-\myhako\right)
\end{align*}

ここで，7と5は互いに素であるから，解 $(x,~y)$ は0以上の整数 $m$ を用いて，

\begin{align*}
\begin{cases}
x=\myhako m+\myhako \\[4pt]y=\myhako m+\myhako
\end{cases}(m=0,~1,~2,~\cdots)
\end{align*}

と表すことができる。
(2) $x,~y$ の最大公約数が3のとき，$x=3X,~y=3Y$ とおくと，

\begin{align*}
7X-5Y=1
\end{align*}

が成り立つから，解 $(X,~Y)$ は0以上の整数 $n$ を用いて，

\begin{align*}
\begin{cases}
X=\myhako n+\myhako \\[4pt]Y=\myhako n+\myhako
\end{cases}(n=0,~1,~2,~\cdots)
\end{align*}

となる。
さらに $x,~y$ の最小公倍数が264であるとき，

\begin{align*}
XY=\myhako
\end{align*}

であるから，$(x,~y)=\left(\myhako,~\myhako\right)$ である。

プリントを次のリンクからダウンロードできます。

ダウンロード

【(1)の考え方と解答】
　$7x-5y=3$ を $7\left(x-\myhako\right)=5\left(y-\myhako\right)$ の形にしよう。
この空欄の意味を考えるために，文字を使って $7(x-a)=5(y-b)$ と書くと，$x=a,~y=b$ のときに「$0=0$」となり，方程式は成り立つから，$x=a,~y=b$ は $7x-5y=3$ の整数解の1つであることが分かる。適当に整数を代入しても，それほど時間がかからず見つけることができるだろう。
　$-5y$ は5の倍数であるから，右辺の3を考えると「$-7+10=3$」という等式を考えることができれば，$x=-1,~y=-2$ が1つの整数解であることが分かる。ただ，今回は空欄の前がマイナスになっているため，他の解を見つけよう。
　「$28-25=3$」という等式を考えることで，別の整数解 $x=4,~y=5$ を見つけることができる。これで $7x-5y=3$ は $7(x-4)=5(y-5)$ と変形できることが分かる。
最初に与えられた方程式 $7x-5y=3$ と変形後の $7(x-4)=5(y-5)$ の形が大きく変わっていて，意味だけを考えると変形方法が見えないから嫌だと感じる人は，次のようにしよう。
$7x-5y=3$ の1つの整数解が $x=4,~y=5$ だと分かっているから，代入しよう。

\begin{align*}
&7x-5y=3~\cdots\cdots① \\[4pt]&7\Cdota4-5\Cdota5=3~\cdots\cdots②
\end{align*}

①が元の方程式で，②が①に解を代入した式。$①-②$ を項ごとに計算すると

\begin{align*}
7(x-4)-5(y-5)=0
\end{align*}

となる。このように，項ごとに計算する方法は重要なので，身に付けておこう。$5(y-5)$ を右辺に移項することで

\begin{align*}
7(x-4)=5(y-5)
\end{align*}

と変形することができる。
それでは整数解 $x,~y$ を求めよう。7と5が互いに素であるから，$x-4$ は5の倍数で，$y-5$ は7の倍数である。今回は整数を表す文字として $m$ を使えといわれているので

\begin{align*}
&\begin{cases}
x-4=5m \\[4pt]y-5=7m
\end{cases} \\[4pt]&\begin{cases}
x=5m+4 \\[4pt]y=7m+5
\end{cases}
\end{align*}

(2) $x,~y$ の最大公約数が3のとき，$x=3X,~y=3Y$ とおくと，
\begin{align*}
7X-5Y=1
\end{align*}
が成り立つから，解 $(X,~Y)$ は0以上の整数 $n$ を用いて，
\begin{align*}
\begin{cases}
X=\myhako n+\myhako \\[4pt]Y=\myhako n+\myhako
\end{cases}(n=0,~1,~2,~\cdots)
\end{align*}
となる。
さらに $x,~y$ の最小公倍数が264であるとき，
\begin{align*}
XY=\myhako
\end{align*}
であるから，$(x,~y)=\left(\myhako,~\myhako\right)$ である。

【(2)の考え方と解答】
誘導にしたがって，解き進めていこう。
$x,~y$ の最大公約数が3のとき，$x=3X,~y=3Y$ とおけて $(*)$ より

\begin{align*}
&7\Cdota3X-5\Cdota3Y=3 \\[4pt]&7X-5Y=1
\end{align*}

となる。(1)と同じようにして，この方程式の整数解を1つ見つけよう。$X,~Y$ を表す空欄の形から判断すると，正の解を見つけないといけないことが分かる。
　$21-20=1$ を考えて，整数解の1つ $X=3,~Y=4$ を見つけることができたから，方程式を

\begin{align*}
7(X-3)=5(Y-4)
\end{align*}

に変形することができる。7と5が互いに素であるから

\begin{align*}
&\begin{cases}
X-3=5n \\[4pt]Y-4=7n
\end{cases}\\[4pt]&\begin{cases}
X=5n+3 \\[4pt]Y=7n+4
\end{cases}(n=0,~1,~2,\cdots)~\cdots\cdots③
\end{align*}

さらに「$x,~y$ の最小公倍数が264」という条件が与えられたから，$x$ と $y$ の積は最大公約数と最小公倍数の積に等しいことを利用しよう。

\begin{align*}
&xy=3\times264 \\[4pt]&3X\Cdota3Y=3\times264 \\[4pt]&XY=88
\end{align*}

$x,~y$ の最大公約数が3で，$x=3X,~y=3Y$ とおいているから，$X$ と $Y$ は互いに素である。88を素因数分解すると

\begin{align*}
88=2^3\Cdota11
\end{align*}

であるから $X$ と $Y$ の組は，1と $2^3\Cdot11$，$2^3$ と11のどちらかである。このうち，③を満たすのは，$X=5n+3=8$, $Y=7n+4=11$ であり，$n=1$ となる。このとき，

\begin{align*}
x=3X=24,~y=3Y=33
\end{align*}

したがって，$(x,~y)=(24,~33)$