ここではユークリッドの互除法について説明します。
ユークリッドの互除法は最大公約数を求める1つの方法です。
比較的大きな2数の最大公約数を求めるのは難しいのですが,ユークリッドの互除法を利用することで,必ず最大公約数を求めることができます。
また,方程式の整数解を求める問題においても役に立ちます。
ユークリッドの互除法とは

ヒロ
ユークリッドの互除法とは,次のようなものである。
ユークリッドの互除法ユークリッドの互除法で,整数 $a,~b$ の最大公約数を求めるには,次の手順を繰り返せばよい。
① $a$ を $b$ で割ったときの余りを $r$ とする。
② $r=0$ ならば,$b$ が $a$ と $b$ の最大公約数である。
$r>0$ ならば,$a$ を $b$ に,$b$ を $r$ に置き換えて,①に戻る。
この手順を繰り返すと,余り $r$ が小さくなり,いつかは $r=0$ になって必ず終了する。
① $a$ を $b$ で割ったときの余りを $r$ とする。
② $r=0$ ならば,$b$ が $a$ と $b$ の最大公約数である。
$r>0$ ならば,$a$ を $b$ に,$b$ を $r$ に置き換えて,①に戻る。
この手順を繰り返すと,余り $r$ が小さくなり,いつかは $r=0$ になって必ず終了する。
ユークリッドの互除法を使う練習

ヒロ
ユークリッドの互除法の仕組みを理解する前に,簡単に最大公約数を求めることができる2数で,ユークリッドの互除法を使って最大公約数を求めることができることを確認しよう。
【ユークリッドの互除法を使ってみる】
ユークリッドの互除法を使って,18と48の最大公約数を求めてみよう。
$a=48,~b=18$ として,$a\div b$ の余りを求める。
次は $a=18,~b=12$ として同じことを繰り返す。
さらに $a=12,~b=6$ とすると
$r=0$ となったときの $b$ は $b=6$ であるから,18と48の最大公約数は6ということが分かる。
ユークリッドの互除法を使って,18と48の最大公約数を求めてみよう。
$a=48,~b=18$ として,$a\div b$ の余りを求める。
\begin{align*}
48=18\times2+12
\end{align*}
よって,$r=12$ である。48=18\times2+12
\end{align*}
次は $a=18,~b=12$ として同じことを繰り返す。
\begin{align*}
18=12\times1+6
\end{align*}
となるから,$r=6$18=12\times1+6
\end{align*}
さらに $a=12,~b=6$ とすると
\begin{align*}
12=6\times2
\end{align*}
となるから $r=0$ となり終了である。12=6\times2
\end{align*}
$r=0$ となったときの $b$ は $b=6$ であるから,18と48の最大公約数は6ということが分かる。
ユークリッドの互除法を理解しよう

ヒロ
それでは,ユークリッドの互除法で最大公約数を求めることができる理由・仕組みを理解しよう。

ヒロ
さっきの2数18と48で考えてみよう。
【ユークリッドの互除法の理解】
長方形の面積を考えることで,視覚的にユークリッドの互除法を理解しよう。
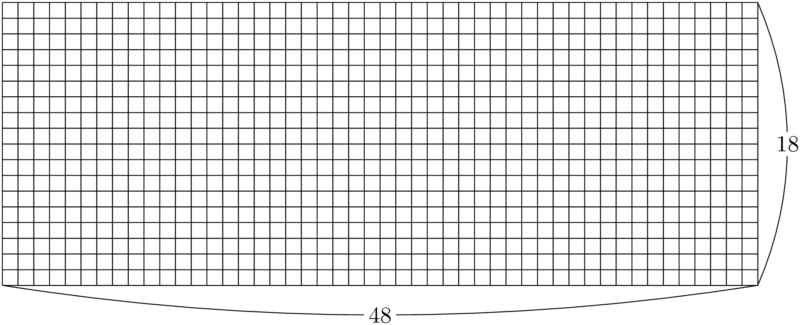
長方形の面積として考えることで,「公約数」は $48\times18$ の長方形を敷きつめることができる正方形の1辺の長さを表すことになる。上図を見ると分かるように,1辺の長さが1の正方形で $48\times18$ の長方形を敷きつめることができるから,1は48と18の1つの公約数である。
数ある公約数の中で48と18の「最大公約数」は, $48\times18$ の長方形を敷きつめることができる正方形の1辺の長さの中で最大のものを表すことになる。
そこで,まずは長さが短い縦の長さ18を1辺の長さとする正方形を考えてみる。これで $48\times18$ の長方形を敷きつめることができれば,18が48と18の最大公約数となる。実際に1辺の長さが18の正方形で分けていくと次のようになる。

これが最初の計算
次に,右に余った $12\times18$ の長方形を12を1辺の長さとする正方形で敷きつめられるかどうかを考える。
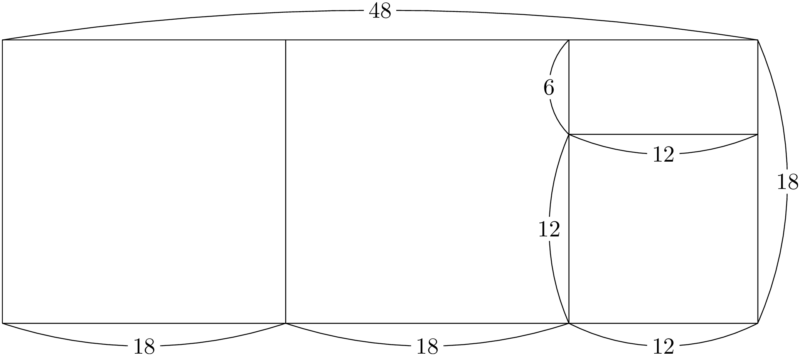
1辺が12の正方形でも敷きつめることができずに $12\times6$ の長方形が余った。これが
それでは,余った $12\times6$ の長方形を1辺の長さが6の正方形で敷きつめられるかどうかを考える。
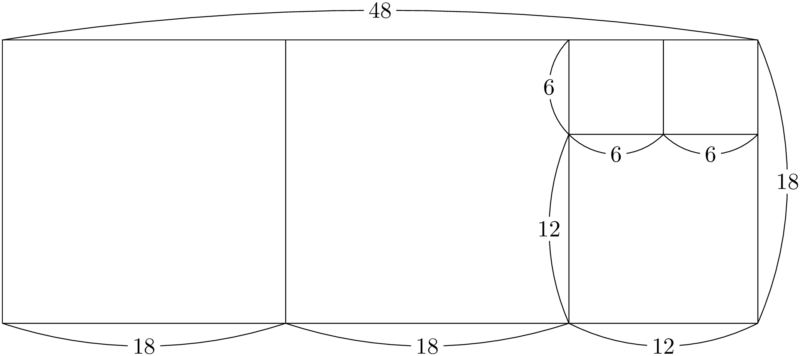
実際に $12\times6$ の長方形を1辺の長さが6の正方形で敷きつめられることが分かる。これが
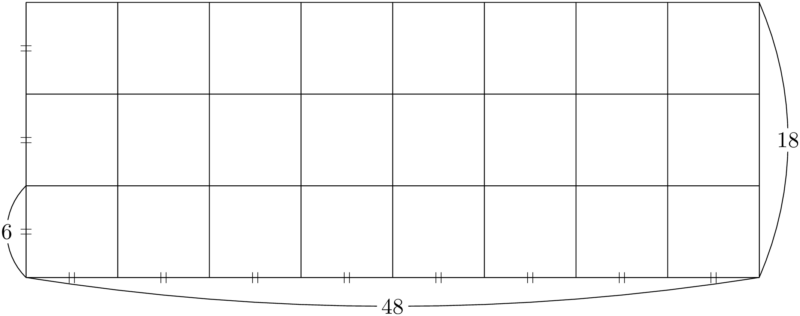
長方形の面積を考えることで,視覚的にユークリッドの互除法を理解しよう。

長方形の面積として考えることで,「公約数」は $48\times18$ の長方形を敷きつめることができる正方形の1辺の長さを表すことになる。上図を見ると分かるように,1辺の長さが1の正方形で $48\times18$ の長方形を敷きつめることができるから,1は48と18の1つの公約数である。
数ある公約数の中で48と18の「最大公約数」は, $48\times18$ の長方形を敷きつめることができる正方形の1辺の長さの中で最大のものを表すことになる。
そこで,まずは長さが短い縦の長さ18を1辺の長さとする正方形を考えてみる。これで $48\times18$ の長方形を敷きつめることができれば,18が48と18の最大公約数となる。実際に1辺の長さが18の正方形で分けていくと次のようになる。

これが最初の計算
\begin{align*}
48=18\times2+12
\end{align*}
において,$a=48,~b=18,~r=12$ となる部分である。48=18\times2+12
\end{align*}
次に,右に余った $12\times18$ の長方形を12を1辺の長さとする正方形で敷きつめられるかどうかを考える。

1辺が12の正方形でも敷きつめることができずに $12\times6$ の長方形が余った。これが
\begin{align*}
18=12\times1+6
\end{align*}
において,$a=18,~b=12,~r=6$ となる部分である。18=12\times1+6
\end{align*}
それでは,余った $12\times6$ の長方形を1辺の長さが6の正方形で敷きつめられるかどうかを考える。

実際に $12\times6$ の長方形を1辺の長さが6の正方形で敷きつめられることが分かる。これが
\begin{align*}
12=6\times2
\end{align*}
において,$a=12,~b=6,~r=0$ となる部分である。12=6\times2
\end{align*}

最大公約数を求める問題
2019年 順天堂大1050と819の最大公約数をユークリッドの互除法を用いて求めよ。
【考え方と解答】
「ユークリッドの互除法を用いて」と書かれているため,その指示に従っていない方法で最大公約数を求めても点数はほとんど貰えないから注意しよう。
「ユークリッドの互除法を用いて」と書かれているため,その指示に従っていない方法で最大公約数を求めても点数はほとんど貰えないから注意しよう。
\begin{align*}
&1050=819\times1+231 \\[4pt]
&819=231\times3+126 \\[4pt]
&231=126\times1+105 \\[4pt]
&126=105\times1+21 \\[4pt]
&105=21\times5
\end{align*}
したがって,1050と819の最大公約数は21である。&1050=819\times1+231 \\[4pt]
&819=231\times3+126 \\[4pt]
&231=126\times1+105 \\[4pt]
&126=105\times1+21 \\[4pt]
&105=21\times5
\end{align*}
最大公約数を求める問題2
2019年 立教大14351と14803の最大公約数は $\myhako$ である。
【考え方と解答】
空欄を埋めるだけなので,最大公約数を暗算で求められる人はサクッと埋めてしまおう。
僕にはそんなことはできないので,ユークリッドの互除法に頼ることにする。
空欄を埋めるだけなので,最大公約数を暗算で求められる人はサクッと埋めてしまおう。
僕にはそんなことはできないので,ユークリッドの互除法に頼ることにする。
\begin{align*}
&14803=14351\times1+452 \\[4pt]
&14351=452\times31+339 \\[4pt]
&452=339\times1+113 \\[4pt]
&339=113\times3
\end{align*}
よって,最大公約数は113である。&14803=14351\times1+452 \\[4pt]
&14351=452\times31+339 \\[4pt]
&452=339\times1+113 \\[4pt]
&339=113\times3
\end{align*}
最大公約数に関する問題
2019年 同志社女子大$n$ は自然数とする。2数 $5n+17$ と $4n+15$ の最大公約数が7になるような $n$ のうち,2桁の数で最大のものは $n=\myhako$ である。
【考え方と解答】
$n$ の式であっても,互除法を同じように利用しよう。
書きやすさを考慮して,2つの自然数 $a,~b$ の最大公約数を $g(a,~b)$ と表すことにする。互除法より,
$n$ の式であっても,互除法を同じように利用しよう。
書きやすさを考慮して,2つの自然数 $a,~b$ の最大公約数を $g(a,~b)$ と表すことにする。互除法より,
\begin{align*}
g(5n+17,~4n+15)&=g((5n+17)-(4n+15),~4n+15) \\[4pt]
&=g(n+2,~4n+15) \\[4pt]
&=g(4n+15,~n+2) \\[4pt]
&=g((4n+15)-4(n+2),~n+2) \\[4pt]
&=g(7,~n+2)
\end{align*}
よって,$5n+17$ と $4n+15$ の最大公約数が7になるのは,自然数 $k$ を用いてg(5n+17,~4n+15)&=g((5n+17)-(4n+15),~4n+15) \\[4pt]
&=g(n+2,~4n+15) \\[4pt]
&=g(4n+15,~n+2) \\[4pt]
&=g((4n+15)-4(n+2),~n+2) \\[4pt]
&=g(7,~n+2)
\end{align*}
\begin{align*}
n+2=7k
\end{align*}
と表せるときである。$n$ は2桁の整数であるから,$n\leqq99$ であり,このときn+2=7k
\end{align*}
\begin{align*}
&7k\leqq99+2 \\[4pt]
&k\leqq\dfrac{101}{7}=14.4\cdots
\end{align*}
したがって,最大の $k$ の値は $k=14$ であるから,求める $n$ の値は&7k\leqq99+2 \\[4pt]
&k\leqq\dfrac{101}{7}=14.4\cdots
\end{align*}
\begin{align*}
n&=7k-2 \\[4pt]
&=7\times14-2 \\[4pt]
&=96
\end{align*}
n&=7k-2 \\[4pt]
&=7\times14-2 \\[4pt]
&=96
\end{align*}


















