Contents
不定方程式の問題3【慶應義塾大】
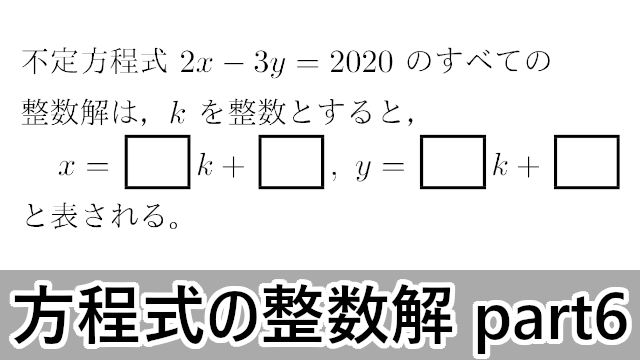
2020年 慶應義塾大不定方程式 $2x-3y=2020$ のすべての整数解は,$k$ を整数とすると,
\begin{align*}
x=\myhako\, k+\myhako,~y=\myhako\, k+\myhako
\end{align*}
と表される。x=\myhako\, k+\myhako,~y=\myhako\, k+\myhako
\end{align*}
【考え方と解答】
右辺を1にした $2x-3y=1$ の整数解を見つけて両辺に2020をかけても良いが,計算が面倒になりそうだから,別の方法で解くことにする。$2x-3y=2020$ より
右辺を1にした $2x-3y=1$ の整数解を見つけて両辺に2020をかけても良いが,計算が面倒になりそうだから,別の方法で解くことにする。$2x-3y=2020$ より
\begin{align*}
x&=\dfrac{3y+2020}{2} \\[4pt]
&=y+1010+\dfrac{y}{2}
\end{align*}
$x,~y$ は整数であるから,$\dfrac{y}{2}$ は整数である。よって $\dfrac{y}{2}=k$ とおくとx&=\dfrac{3y+2020}{2} \\[4pt]
&=y+1010+\dfrac{y}{2}
\end{align*}
\begin{align*}
&y=2k
\end{align*}
となり,このとき&y=2k
\end{align*}
\begin{align*}
x&=2k+1010+k \\[4pt]
&=3k+1010
\end{align*}
よってx&=2k+1010+k \\[4pt]
&=3k+1010
\end{align*}
\begin{align*}
\begin{cases}
x=3k+1010 \\[4pt]
y=2k+0
\end{cases}
\end{align*}
\begin{cases}
x=3k+1010 \\[4pt]
y=2k+0
\end{cases}
\end{align*}

ヒロ
空欄に「0」が入ることがあるのが鬱陶しいが仕方ない。