方程式の整数解 －不定方程式－【芝浦工大・昭和薬科大・慶應義塾大】

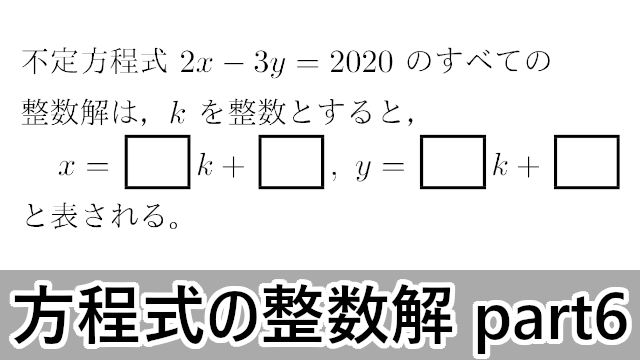
Contents

不定方程式の問題2【昭和薬科大】

2018年昭和薬科大$125x-64y=-3$ を満たすすべての整数解は $\myhako$ である。

【考え方と解答】
整数解の1つを見つけることが難しいと感じる場合は，右辺を1にした方程式「$125x-64y=1$」の整数解をユークリッドの互除法を利用して見つけよう。

\begin{align*}
&125=64\times1+61 \\[4pt]
&64=61\times1+3 \\[4pt]
&61=3\times20+1
\end{align*}

これらの計算より

\begin{align*}
1&=61-3\times20 \\[4pt]
&=61-(64-61)\times20 \\[4pt]
&=61\times21-64\times20 \\[4pt]
&=(125-64)\times21-64\times20 \\[4pt]
&=125\times21-64\times41
\end{align*}

よって $125x-64y=1$ の1つの整数解が $x=21,~y=41$ であることが分かった。
この結果から，$125x-64y=-3$ の解を求めるために，$125\Cdot21-64\Cdot41=1$ の両辺に $-3$ をかける。

\begin{align*}
&125\Cdota21\Cdota(-3)-64\Cdota41\Cdot(-3)=1\Cdota(-3) \\[4pt]
&125\Cdota(-63)-64\Cdota(-123)=-3
\end{align*}

これで $125x-64y=-3$ の整数解の1つとして，$x=-63,~y=-123$ を見つけることができたから，同じように変形して

\begin{align*}
125(x+63)-64(y+123)=0
\end{align*}

125と64が互いに素であるから，整数 $n$ を用いて

\begin{align*}
&\begin{cases}
x+63=64n \\[4pt]
y+123=125n
\end{cases} \\[4pt]
&\begin{cases}
x=64n-63 \\[4pt]
y=125n-123
\end{cases}
\end{align*}

このままでも間違いではないが，無駄に定数項が大きいのが気になる人は，次のようにして少し変えよう。

\begin{align*}
x&=64n-63 \\[4pt]
&=64(n-1)+1
\end{align*}

と変形すると，$n-1$ は整数だから，新たに $k$ とおくと $x=64k-1$ と表すことができる。同じように $y$ は

\begin{align*}
y&=125(n-1)+2 \\[4pt]
&=125k+2
\end{align*}

となる。この結果から，$k=0$ のとき $(x,~y)=(1,~2)$ となり，最初に見つけた整数解よりずっと簡単な値の整数解があったことが分かる。

ヒロ

一般に，右辺の値が1の不定方程式の整数解を見つけてから，右辺の値を揃えるために定数をかけて整数解を求めると，かなり大きな値の整数解になってしまう。

ヒロ

これを避ける方法としては，互除法に頼らない解法が有効かもしれない。

【別の考え方と解答】
$125x-64y=-3$ より

\begin{align*}
y&=\dfrac{125x+3}{64} \\[4pt]
&=2x+\dfrac{-3x+3}{64} \\[4pt]
&=2x-\dfrac{3(x-1)}{64}
\end{align*}

$x,~y$ が整数だから $\dfrac{x-1}{64}$ は整数である。$\dfrac{x-1}{64}=k$ とおくと

\begin{align*}
&x-1=64k \\[4pt]
&x=64k+1
\end{align*}

このとき

\begin{align*}
y&=2x-3k \\[4pt]
&=2(64k+1)-3k \\[4pt]
&=125k+2
\end{align*}