2016年センター試験 数学ⅡB 第2問微積の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
放物線 $y=\dfrac14x^2$ を $C_2$ とする。
(1) 実数 $a$ に対して,2直線 $x=a,~x=a+1$ と $C_1,~C_2$ で囲まれた図形 $D$ の面積 $S$ は
S&=\dint{a}{a+1}\left(\dfrac{1}{\myBox{ア}}~x^2+\dfrac{1}{\myBox{イ}}\right)\;dx \\[4pt]
&=\dfrac{a^2}{\myBox{ウ}}+\dfrac{a}{\myBox{エ}}+\dfrac{\myBox{オ}}{\myBox{カキ}}
\end{align*}
である。$S$ は $a=\dfrac{\myBox{クケ}}{\myBox{コ}}$ で最小値 $\dfrac{\myBox{サシ}}{\myBox{スセ}}$ をとる。
(2) 4点 $(a,~0),~(a+1,~0),~(a+1,~1),~(a,~1)$ を頂点とする正方形を $R$ で表す。$a$ が $a\geqq0$ の範囲を動くとき,正方形 $R$ と(1)の図形 $D$ の共通部分の面積を $T$ とおく。$T$ が最大となる $a$ の値を求めよう。
直線 $y=1$ は,$C_1$ と $\left(\pm\myBox{ソ},~1\right)$で,$C_2$ と $\left(\pm\myBox{タ},~1\right)$で交わる。
したがって,正方形 $R$ と図形 $D$ の共通部分が空集合にならないのは,$0\leqq a\leqq\myBox{チ}$ のときである。
$\mybox{ソ}\leqq a\leqq\mybox{チ}$ のとき,正方形 $R$ は放物線 $C_1$ と $x$ 軸の間にあり,この範囲で $a$ が増加するとき,$T$ は $\myBox{ツ}$。$\mybox{ツ}$ に当てはまるものを,次の⓪~②のうちから一つ選べ。
⓪ 増加する ① 減少する ② 変化しない
したがって,$T$ が最大になる $a$ の値は,$0\leqq a\leqq\mybox{ソ}$ の範囲にある。
$0\leqq a\leqq\mybox{ソ}$ のとき,(1)の図形 $D$ のうち,正方形 $R$ の外側にある部分の面積 $U$ は
U=\dfrac{a^3}{\myBox{テ}}+\dfrac{a^2}{\myBox{ト}}
\end{align*}
T=-\dfrac{a^3}{\myBox{ナ}}-\dfrac{a^2}{\myBox{ニ}}+\dfrac{a}{\myBox{ヌ}}+\dfrac{\mybox{オ}}{\mybox{カキ}}
\end{align*}
a=\dfrac{\myBox{ネノ}+\sqrt{\myBox{ハ}}}{\myBox{ヒ}}
\end{align*}
(1)の解答

最初は図形 $D$ の面積を求める問題。定積分で求めよう。
$a\leqq x\leqq a+1$ において,$C_1$ が $C_2$ の上側にあるから
S&=\dint{a}{a+1}\left(\dfrac{1}{2}x^2+\dfrac{1}{2}-\dfrac{1}{4}x^2\right)\;dx \\[4pt]
&=\dint{a}{a+1}\left(\dfrac{1}{4}x^2+\dfrac{1}{2}\right)\;dx \\[4pt]
&=\Tint{\dfrac{1}{12}x^3+\dfrac{1}{2}x}{a}{a+1} \\[4pt]
&=\dfrac{(a+1)^3-a^3}{12}+\dfrac{(a+1)-a}{2} \\[4pt]
&=\dfrac{3a^2+3a+1}{12}+\dfrac{1}{2} \\[4pt]
&=\dfrac{a^2}{4}+\dfrac{a}{4}+\dfrac{7}{12}
\end{align*}

定積分では,各項ごとに上端と下端を代入して計算した方が,分母が揃っていて計算しやすくなることが多い。

次は $S$ を $a$ の2次関数とみて,最小値を求める問題。グラフは下に凸の放物線であり,$a$ はすべての実数を取り得るから,頂点で最小値を取ることが分かる。
軸の方程式は,$a=-\dfrac{1}{2}$ であるから,$S$ は $a=\dfrac{-1}{2}$ で最小値をとり,最小値は
\dfrac{7}{12}-\dfrac{1}{4}\Cdota\left(\dfrac{1}{2}\right)^2=\dfrac{25}{48}
\end{align*}

最小値は頂点の $y$ 座標に等しいから,今回は2次関数の2乗に比例する性質を利用して求めたよ。
$y=\dfrac{x^2}{4}+\dfrac{x}{4}+\dfrac{7}{12}$ のグラフは軸が $x=-\dfrac{1}{2}$ の下に凸の放物線だから,下図のようになる。
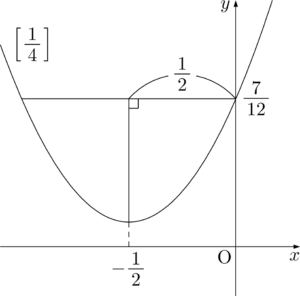
まず,座標を簡単に求めることができる点は $y$ 切片の点 $\mathrm{A}\left(0,~\dfrac{7}{12}\right)$ である。点Aと直線 $x=-\dfrac{1}{2}$ との距離が $\dfrac{1}{2}$ で,$x^2$ の係数が $\dfrac{1}{4}$ だから,頂点の $y$ は
\dfrac{7}{12}-\dfrac{1}{4}\Cdota\left(\dfrac{1}{2}\right)^2
\end{align*}
(2)の解答
(2) 4点 $(a,~0),~(a+1,~0),~(a+1,~1),~(a,~1)$ を頂点とする正方形を $R$ で表す。$a$ が $a\geqq0$ の範囲を動くとき,正方形 $R$ と(1)の図形 $D$ の共通部分の面積を $T$ とおく。$T$ が最大となる $a$ の値を求めよう。
直線 $y=1$ は,$C_1$ と $\left(\pm\myBox{ソ},~1\right)$で,$C_2$ と $\left(\pm\myBox{タ},~1\right)$で交わる。
したがって,正方形 $R$ と図形 $D$ の共通部分が空集合にならないのは,$0\leqq a\leqq\myBox{チ}$ のときである。
$\mybox{ソ}\leqq a\leqq\mybox{チ}$ のとき,正方形 $R$ は放物線 $C_1$ と $x$ 軸の間にあり,この範囲で $a$ が増加するとき,$T$ は $\myBox{ツ}$。$\mybox{ツ}$ に当てはまるものを,次の⓪~②のうちから一つ選べ。
⓪ 増加する ① 減少する ② 変化しない
したがって,$T$ が最大になる $a$ の値は,$0\leqq a\leqq\mybox{ソ}$ の範囲にある。
$0\leqq a\leqq\mybox{ソ}$ のとき,(1)の図形 $D$ のうち,正方形 $R$ の外側にある部分の面積 $U$ は\begin{align*}である。よって,$0\leqq a\leqq\mybox{ソ}$ において
U=\dfrac{a^3}{\myBox{テ}}+\dfrac{a^2}{\myBox{ト}}
\end{align*}\begin{align*}である。①の右辺の増減を調べることにより,$T$ は
T=-\dfrac{a^3}{\myBox{ナ}}-\dfrac{a^2}{\myBox{ニ}}+\dfrac{a}{\myBox{ヌ}}+\dfrac{\mybox{オ}}{\mybox{カキ}}
\end{align*}\begin{align*}で最大値をとることがわかる。
a=\dfrac{\myBox{ネノ}+\sqrt{\myBox{ハ}}}{\myBox{ヒ}}
\end{align*}

まずは直線 $y=1$ と $C_1,~C_2$ の交点をそれぞれ求めよう。
$\dfrac{1}{2}x^2+\dfrac{1}{2}=1$ より
&x^2=1 \\[4pt]
&x=\pm1
\end{align*}
&x^2=4 \\[4pt]
&x=\pm2
\end{align*}

正方形 $R$ と図形 $D$ を図示して考えよう。
図形 $D$ は次の図の斜線部分である。青い部分が $R$ と $D$ の共通部分である。

この状態から $a$ を大きくしていくと,正方形 $R$ が右へ動いていく。それと同時に,図形 $D$ も右へ動いていく。$a=1$ のときは下図のようになる。

さらに $a$ の値を大きくしていくと,$a>2$ のときに共通部分が空集合になることが分かる。よって,正方形 $R$ と図形 $D$ の共通部分が空集合にならないのは,$0\leqq a\leqq2$ のときである。

次は $T$ の変化を考える問題。これは図を考えれば簡単だろう。
上の $a=1$ の状態から,$a$ の値を大きくすると,下図のようになる。

$1\leqq a\leqq2$ の範囲で $a$ が増加すると,共通部分の面積 $T$ が減少することが分かる。よって,$\myBox{ツ}=①$

ここまでの流れで,$T$ が最大になる $a$ の値が $0\leqq a\leqq1$ の範囲にあることが分かるね。

逆にこの記述によって,$\myBox{ツ}$ の答えが分かってしまう。先にこれを読んでいれば楽だったなという思いもあるけど,答えが合っていると確信できるため,安心できる。

次は $U$ を求めよう。
下図の緑の部分の面積が $U$ である。
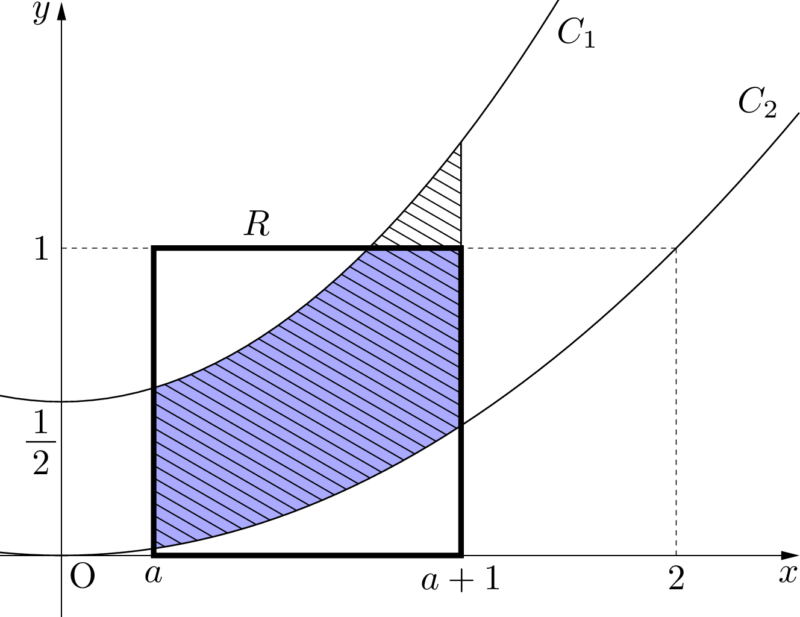
よって,
U&=\dint{1}{a+1}\left\{\left(\dfrac{1}{2}x^2+\dfrac{1}{2}\right)-1\right\}\;dx \\[4pt]
&=\dint{1}{a+1}\left(\dfrac{1}{2}x^2-\dfrac{1}{2}\right)\;dx \\[4pt]
&=\Tint{\dfrac{1}{6}x^3-\dfrac{1}{2}x}{1}{a+1} \\[4pt]
&=\dfrac{(a+1)^3-1}{6}-\dfrac{(a+1)-1}{2} \\[4pt]
&=\dfrac{a^3}{6}+\dfrac{a^2}{2}
\end{align*}

最後の計算は空欄を見た上で計算している。空欄を見ることで,$a$ と定数項が消えることが分かるから,$a^3$ と $a^2$ の係数を求めれば空欄を埋めることができる。

計算が合っているかのチェックとして,$a$ と定数項が消えることを確認すると良い。

次は $T$ を求める問題。問題文に「よって」とあるから,$U$ が求まったことによって,$T$ を求めることができることが分かる。

いま $U$ が緑の部分の面積で,$T$ 青い部分の面積。ということは,$U+T=S$ となることが分かるね。
$0\leqq a\leqq1$ のとき,$S=U+T$ より
T&=S-U \\[4pt]
&=\left(\dfrac{a^2}{4}+\dfrac{a}{4}+\dfrac{7}{12}\right)-\left(\dfrac{a^3}{6}+\dfrac{a^2}{2}\right) \\[4pt]
&=-\dfrac{a^3}{6}-\dfrac{a^2}{4}+\dfrac{a}{4}+\dfrac{7}{12}
\end{align*}

最後の $T$ の最大値は微分して求めよう。
\dfrac{dT}{da}&=-\dfrac{a^2}{2}-\dfrac{a}{2}+\dfrac{1}{4}
\end{align*}
&2a^2+2a-1=0 \\[4pt]
&a=\dfrac{-1\pm\sqrt{3}}{2}
\end{align*}
$\dfrac{dT}{da}$ の符号は $a=\dfrac{-1+\sqrt{3}}{2}$ の前後で,正から負に変化するから極大となることが分かる。つまり $a=\dfrac{-1+\sqrt{3}}{2}$ で $T$ は最大値をとることがわかる。
2016年 センター数学IIB微積を解いた感想

センター数学の微積では珍しく,時間を短縮できるような箇所がほとんどない。

(2)の正方形と図形 $D$ の共通部分の問題は,実際に図を描かないとしんどいだろう。

とはいえ,それほど難しくもなく,分量も多くないので,落ち着いて解けば大丈夫だと思う。






















