考える区間が動く場合の3次関数の最大値と最小値に関する問題を解説します。
区間に文字が含まれているため,文字の値によって,区間自体が変化するため,最大値や最小値をとる $x$ の値が変化します。
極値や区間の端点のいずれかで,最大・最小となるため,それらの位置関係に注意して場合分けをすると良いでしょう。
具体的な方法については,問題を解いて習得しましょう。
2021年 高知大
2021年 高知大実数 $x$ に対して,$f(x)=-\dfrac{1}{4}x^3+3x$ とおく。このとき,次の問いに答えよ。
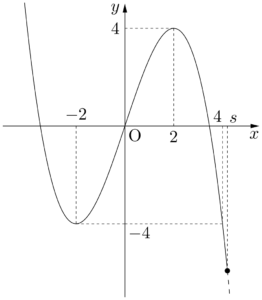
(1) $y=f(x)$ のグラフをかけ。
(2) $f(x-2)=f(x)$ をみたす実数 $x$ をすべて求めよ。
(3) 実数 $s$ に対して,$f(x)$ の $x\leqq s$ の範囲における最小値を $g(s)$ とおく。このとき,$t=g(s)$ のグラフをかけ。
(4) 実数 $s$ に対して,$f(x)$ の $s-2\leqq x\leqq s$ の範囲における最小値を $h(s)$ とおく。このとき,$t=h(s)$ のグラフをかけ。
(1) $y=f(x)$ のグラフをかけ。
(2) $f(x-2)=f(x)$ をみたす実数 $x$ をすべて求めよ。
(3) 実数 $s$ に対して,$f(x)$ の $x\leqq s$ の範囲における最小値を $g(s)$ とおく。このとき,$t=g(s)$ のグラフをかけ。
(4) 実数 $s$ に対して,$f(x)$ の $s-2\leqq x\leqq s$ の範囲における最小値を $h(s)$ とおく。このとき,$t=h(s)$ のグラフをかけ。
【(1)の解答と考え方】
$f(x)=-\dfrac{1}{4}x^3+3x$ のとき
よって,$f(x)$ の増減は次のようになる。
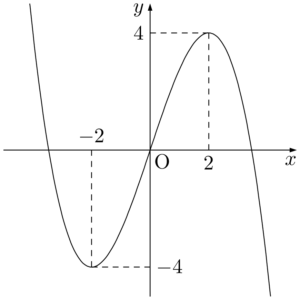
$f(x)=-\dfrac{1}{4}x^3+3x$ のとき
\begin{align*}
f'(x)&=-\dfrac{3}{4}x^2+3 \\[4pt]
&=-\dfrac{3}{4}(x^2-4) \\[4pt]
&=-\dfrac{3}{4}(x-2)(x+2)
\end{align*}
$f'(x)=0$ を解くと,$x=\pm2$f'(x)&=-\dfrac{3}{4}x^2+3 \\[4pt]
&=-\dfrac{3}{4}(x^2-4) \\[4pt]
&=-\dfrac{3}{4}(x-2)(x+2)
\end{align*}
よって,$f(x)$ の増減は次のようになる。
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -2 & \cdots & 2 & \cdots \\\hline
f'(x) & – & 0 & + & 0 & – \\\hline
f(x) & \searrow & 極小 & \nearrow & 極大 & \searrow \\\hline
\end{array}
\end{align*}
したがって,$y=f(x)$ のグラフは次のようになる。\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -2 & \cdots & 2 & \cdots \\\hline
f'(x) & – & 0 & + & 0 & – \\\hline
f(x) & \searrow & 極小 & \nearrow & 極大 & \searrow \\\hline
\end{array}
\end{align*}

(2) $f(x-2)=f(x)$ をみたす実数 $x$ をすべて求めよ。
【(2)の解答と考え方】
$f(x-2)=f(x)$ より
$f(x-2)=f(x)$ より
\begin{align*}
&-\dfrac{1}{4}(x-2)^3+3(x-2)=-\dfrac{1}{4}x^3+3x \\[4pt]
&x^3-(x-2)^3-24=0 \\[4pt]
&6x^2-12x-16=0 \\[4pt]
&3x^2-6x-8=0 \\[4pt]
&x=\dfrac{3\pm\sqrt{33}}{3}
\end{align*}
&-\dfrac{1}{4}(x-2)^3+3(x-2)=-\dfrac{1}{4}x^3+3x \\[4pt]
&x^3-(x-2)^3-24=0 \\[4pt]
&6x^2-12x-16=0 \\[4pt]
&3x^2-6x-8=0 \\[4pt]
&x=\dfrac{3\pm\sqrt{33}}{3}
\end{align*}
(3) 実数 $s$ に対して,$f(x)$ の $x\leqq s$ の範囲における最小値を $g(s)$ とおく。このとき,$t=g(s)$ のグラフをかけ。
【(3)の解答と考え方】
$f(x)=f(-2)$ となる $x$ の値を求める。3次関数のグラフの等間隔性を考えると,$x=4$ であることがすぐに分かるが,計算も書いておく。
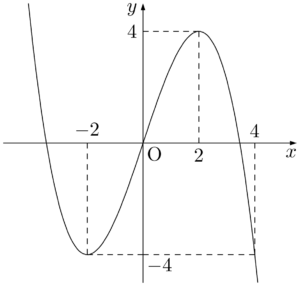
(i) $s<-2$ のとき
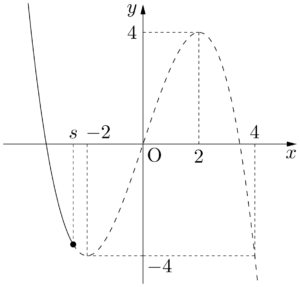
グラフより
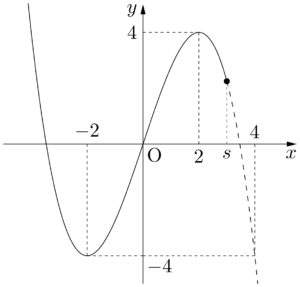
グラフより
グラフより
$f(x)=f(-2)$ となる $x$ の値を求める。3次関数のグラフの等間隔性を考えると,$x=4$ であることがすぐに分かるが,計算も書いておく。
\begin{align*}
&-\dfrac{1}{4}x^3+3x=-4 \\[4pt]
&x^3-12x-16=0
\end{align*}
$f(x)=f(-2)$ の実数解は,$y=f(x)$ のグラフと $y=-2$ のグラフの共有点の $x$ 座標に等しいから,$x=-2$ を重解にもつことが分かるだろう。このことから,$x^3-12x-16$ は $(x+2)^2$ を因数にもつことが分かる。定数項に着目することで簡単に因数分解できる。&-\dfrac{1}{4}x^3+3x=-4 \\[4pt]
&x^3-12x-16=0
\end{align*}
\begin{align*}
&(x+2)^2(x-4)=0 \\[4pt]
&x=-2,~4
\end{align*}
次のグラフを利用して最小値を求めよう。&(x+2)^2(x-4)=0 \\[4pt]
&x=-2,~4
\end{align*}

(i) $s<-2$ のとき

グラフより
\begin{align*} g(s)=f(s)=-\dfrac{1}{4}s^3+3s \end{align*}
(ii) $-2\leqq s\leqq4$ のとき
グラフより
\begin{align*} g(s)=f(-2)=-4 \end{align*}
(iii) $4<s$ のとき
グラフより
\begin{align*} g(s)=f(s)=-\dfrac{1}{4}s^3+3s \end{align*}
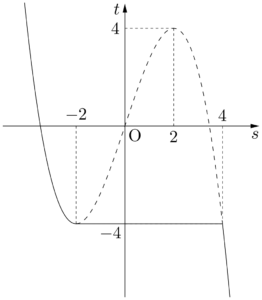
以上より,$t=g(s)$ のグラフは次のようになる。

ヒロ
$t=g(s)$ のグラフを描くだけなら,上のように丁寧に場合分けをする必要はない。

ヒロ
3次関数の最小値は,考えている区間の端点か極小でとるから,このことを考えると,(1)のグラフを見るだけで $t=g(s)$ のグラフを描くことができる。
(4) 実数 $s$ に対して,$f(x)$ の $s-2\leqq x\leqq s$ の範囲における最小値を $h(s)$ とおく。このとき,$t=h(s)$ のグラフをかけ。
【(4)の解答と考え方】
最小値 $h(s)$ は,区間の端点の値 $f(s-2),~f(s)$ か極小値 $f(-2)=-4$ のいずれかである。ただし,極小値が最小値になりうるのは,$-2$ が $s-2\leqq x\leqq s$ に含まれるときである。すなわち
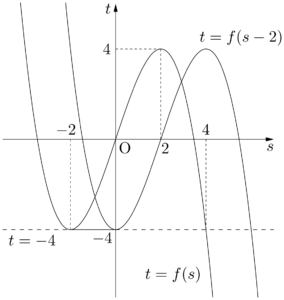
$t=f(s-2),~t=f(s),~t=-4$ のグラフを1つの $st$ 平面上に描くと次のようになる。
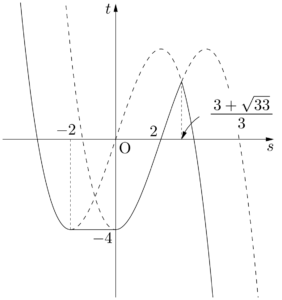
3つのグラフで,それぞれの $s$ の値において,最小になっているものを選んで結んだものが $t=h(s)$ のグラフであり,下図の実線のようになる。
最小値 $h(s)$ は,区間の端点の値 $f(s-2),~f(s)$ か極小値 $f(-2)=-4$ のいずれかである。ただし,極小値が最小値になりうるのは,$-2$ が $s-2\leqq x\leqq s$ に含まれるときである。すなわち
\begin{align*} &s-2\leqq-2\leqq s \\[4pt] &-2\leqq s\leqq0 \end{align*}
のときである。$t=f(s-2),~t=f(s),~t=-4$ のグラフを1つの $st$ 平面上に描くと次のようになる。

3つのグラフで,それぞれの $s$ の値において,最小になっているものを選んで結んだものが $t=h(s)$ のグラフであり,下図の実線のようになる。


ヒロ
(4)の解法のように,グラフを利用して最大値や最小値を求める方法も身に付けておくのが良いだろう。


















