ある円に外接しながら半径が等しい円が滑らずに回転するときの円周上の定点の軌跡をカージオイドといいます。グラフの概形は次のようになります。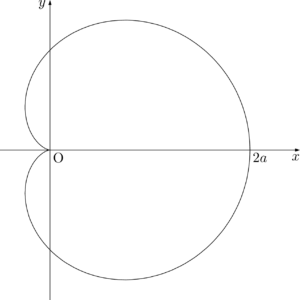
カージオイド曲線の媒介変数表示,曲線の描画,面積,曲線の長さ,回転体の体積について知っておきましょう。
Contents
カージオイド曲線の媒介変数表示

ヒロ
カージオイド上の点 $\mathrm{P}(x,~y)$ の媒介変数表示を導こう。
点 $\mathrm{C}\left(\dfrac{1}{2}a,~0\right)$ を中心とする半径 $\dfrac12a$ の円を $C$ とし,点 $\mathrm{D}_1\left(\dfrac{3}{2}a,~0\right)$ を中心とする半径 $\dfrac12a$ の円を $D$ とする。また,点A,B の座標をそれぞれ $(2a,~0)$,$(a,~0)$ とする。円 $D$ が円 $C$ に外接しながら滑らずに転がり,点 $\mathrm{D}_1$ が $\mathrm{D}_2$ まできたとき,$\kaku{D_1CD_2}=\theta$ とし,接点を $\mathrm{B}_1$ とする。
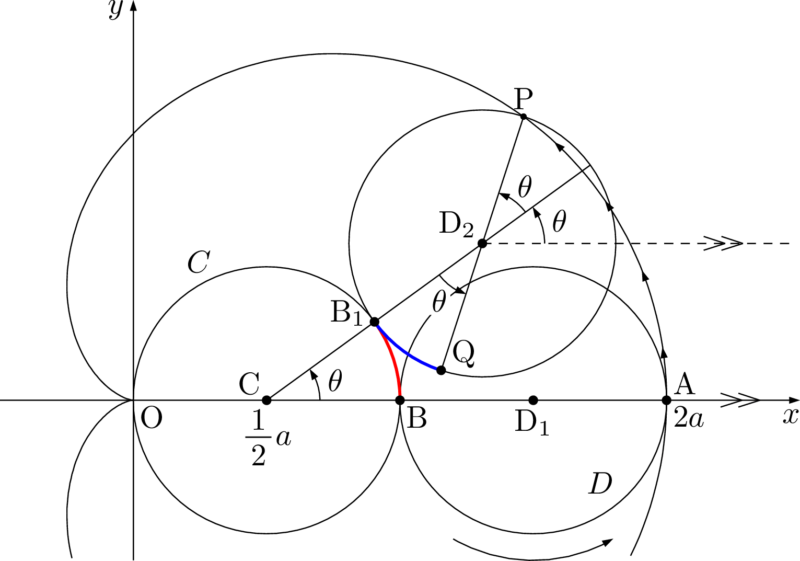
このとき,点Bは点Qの位置にあり,$\ko{\mathrm{BB_1}}=\ko{\mathrm{QB_1}}$ となるから,$\kaku{B_1D_2Q}=\theta$ である。また,点Aは点Pの位置にあることが分かるから,$\mathrm{D_2P}$ と $x$ 軸の正の方向となす角は $2\theta$ となる。

このとき,点Bは点Qの位置にあり,$\ko{\mathrm{BB_1}}=\ko{\mathrm{QB_1}}$ となるから,$\kaku{B_1D_2Q}=\theta$ である。また,点Aは点Pの位置にあることが分かるから,$\mathrm{D_2P}$ と $x$ 軸の正の方向となす角は $2\theta$ となる。
\begin{align*}
\Vec{OP}=\Vec{OC}+\Vec{CD_2}+\Vec{D_2P}
\end{align*}
であるから,点Pの座標を $(x,~y)$ とすると\Vec{OP}=\Vec{OC}+\Vec{CD_2}+\Vec{D_2P}
\end{align*}
\begin{align*}
(x,~y)&=\left(\dfrac{1}{2}a,~0\right)+(a\cos\theta,~a\sin\theta)+\left(\dfrac{1}{2}a\cos2\theta,~\dfrac{1}{2}a\sin2\theta\right) \\[4pt]
&=\left(\dfrac{1}{2}a+a\cos\theta+\dfrac{1}{2}a(2\cos^2\theta-1),~a\sin\theta+a\sin\theta\cos\theta\right) \\[4pt]
&=(a\cos\theta(1+\cos\theta),~a\sin\theta(1+\cos\theta))
\end{align*}
よって(x,~y)&=\left(\dfrac{1}{2}a,~0\right)+(a\cos\theta,~a\sin\theta)+\left(\dfrac{1}{2}a\cos2\theta,~\dfrac{1}{2}a\sin2\theta\right) \\[4pt]
&=\left(\dfrac{1}{2}a+a\cos\theta+\dfrac{1}{2}a(2\cos^2\theta-1),~a\sin\theta+a\sin\theta\cos\theta\right) \\[4pt]
&=(a\cos\theta(1+\cos\theta),~a\sin\theta(1+\cos\theta))
\end{align*}
\begin{align*}
\begin{cases}
x=a\cos\theta(1+\cos\theta) \\[4pt]
y=a\sin\theta(1+\cos\theta)
\end{cases}
\end{align*}
\begin{cases}
x=a\cos\theta(1+\cos\theta) \\[4pt]
y=a\sin\theta(1+\cos\theta)
\end{cases}
\end{align*}


















