ブラーマグプタの公式【円に内接する四角形の面積】

ここではブラーマグプタの公式について説明します。

大学入試問題では，「ブラーマグプタの公式」という公式の名前が出ることは少ないですが，その公式の証明が出題されることがあります。

そのため，ブラーマグプタの公式を知っているかどうかではなく，証明できるかどうかがポイントとなります。

一度は経験しておく方が良いでしょう。

Contents

1 ブラーマグプタの公式
2 2019年京都府立大
3 2019年産業医科大

ブラーマグプタの公式

ヒロ

ブラーマグプタの公式とは次のようなものである。

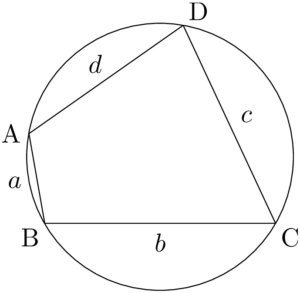
ブラーマグプタの公式円周上に4点A, B, C, Dがあり，$\text{AB}=a$, $\text{BC}=b$, $\text{CD}=c$, $\text{DA}=d$ とする。$s=\dfrac{a+b+c+d}{2}$とすると，四角形ABCDの面積 $S$ は，

\begin{align*}
S=\sqrt{(s-a)(s-b)(s-c)(s-d)}
\end{align*}

と表される。

ヒロ

ちなみに，三角形を四角形の特別な場合と見て $d=0$ とするとヘロンの公式が得られる。

2019年京都府立大

ヒロ

2019年の京都府立大でブラーマグプタの公式の証明が出題されている。

2019年京都府立大以下の問いに答えよ。
(1) $a^4-2a^2b^2-2a^2c^2+b^4-2b^2c^2+c^4$ を因数分解せよ。
(2) 円に内接する四角形ABCDにおいて，$\text{AB}=a$, $\text{BC}=b$, $\text{CD}=c$, $\text{DA}=d$ とする。四角形ABCDの面積は，

\begin{align*}
\dfrac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}
\end{align*}

であることを示せ。

【(1)の考え方と解答】
$a,~b,~c$ の3文字あり，どれについても最高次数が等しいから $a$ に着目して因数分解しよう。

\begin{align*}
(与式)&=a^4-2(b^2+c^2)a^2+b^4-2b^2c^2+c^4 \\[4pt]
&=a^4-2(b^2+c^2)a^2+(b^2-c^2)^2 \\[4pt]
&=\{a^2-(b+c)^2\}\{a^2-(b-c)^2\} \\[4pt]
&=(a+b+c)(a-b-c)(a+b-c)(a-b+c)
\end{align*}

(2) 円に内接する四角形ABCDにおいて，$\text{AB}=a$, $\text{BC}=b$, $\text{CD}=c$, $\text{DA}=d$ とする。四角形ABCDの面積は，
\begin{align*}
\dfrac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}
\end{align*}
であることを示せ。

【(2)の考え方と解答】
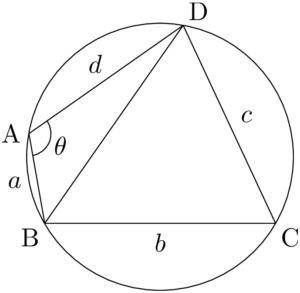
対角線を引いて2つの三角形に分割して面積を求めよう。
$\kaku{BAD}=\theta$ とし，四角形ABCDの面積を $S$ とする。

\begin{align*}
S&=\sankaku{ABD}+\sankaku{BCD} \\[4pt]
&=\dfrac{1}{2}ad\sin\theta+\dfrac{1}{2}bc\sin(180\Deg-\theta) \\[4pt]
&=\dfrac{1}{2}(ad+bc)\sin\theta~\cdots\cdots①
\end{align*}

$\sankaku{ABD}$ と $\sankaku{BCD}$ において，余弦定理を用いると

\begin{align*}
&\text{BD}^2=a^2+d^2-2ad\cos\theta \\[4pt]
&\text{BD}^2=b^2+c^2-2bc\cos(180\Deg-\theta) \\[4pt]
&\qquad =b^2+c^2+2bc\cos\theta
\end{align*}

2式から $\text{BD}^2$ を消去して

\begin{align*}
&a^2+d^2-2ad\cos\theta=b^2+c^2+2bc\cos\theta \\[4pt]
&\cos\theta=\dfrac{a^2+d^2-b^2-c^2}{2(ad+bc)} \\[4pt]
&\cos^2\theta=\dfrac{(a^2+d^2-b^2-c^2)^2}{4(ad+bc)^2}
\end{align*}

$\sin\theta>0$ であるから

\begin{align*}
\sin\theta&=\sqrt{1-\cos^2\theta} \\[4pt]
&=\sqrt{1-\dfrac{(a^2+d^2-b^2-c^2)^2}{4(ad+bc)^2}} \\[4pt]
&=\dfrac{\sqrt{4(ad+bc)^2-(a^2+d^2-b^2-c^2)^2}}{2(ad+bc)} \\[4pt]
&=\dfrac{\sqrt{\{2(ad+bc)+(a^2+d^2-b^2-c^2)\}\{2(ad+bc)-(a^2+d^2-b^2-c^2)\}}}{2(ad+bc)} \\[4pt]
&=\dfrac{\sqrt{\{(a+d)^2-(b-c)^2\}\{(b+c)^2-(a-d)^2\}}}{2(ad+bc)} \\[4pt]
&=\dfrac{\sqrt{(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)}}{2(ad+bc)}~\cdots\cdots②
\end{align*}

②を①に代入すると

\begin{align*}
S&=\dfrac{1}{4}\sqrt{(a+d+b-c)(a+d-b+c)(b+c+a-d)(b+c-a+d)} \\[4pt]
&=\dfrac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}
\end{align*}

よって，示された。