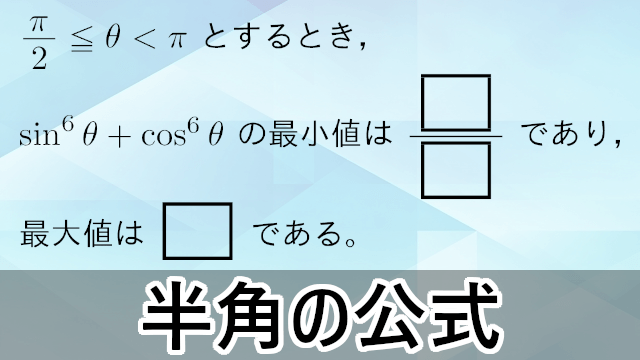
ここでは,三角関数の半角の公式について説明します。
三角関数の半角の公式は,2倍角の公式と同様に,加法定理から導かれますが,覚えて使いこなせるようにしましょう。
半角の公式は「次数を下げるための式」として使われることがあることも覚えておくと良いでしょう。
Contents
半角の公式

ヒロ
半角の公式とは次のようなものである。
自由入力

ヒロ
サインとコサインで,符号がどっちだったっけ・・・となってしまうが,解決策を2つ紹介しておく。
【$\theta$ に適当な値を代入する】
$\theta=0$ を代入すると,$\sin0=0$ であるから,$\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}$ と分かる。$\cos0=1$ であるから,$\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2}$ と分かる。
$\theta=0$ でなくても,$\theta=\dfrac{\pi}{2}$ を代入するのもアリ。
$\theta=0$ を代入すると,$\sin0=0$ であるから,$\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}$ と分かる。$\cos0=1$ であるから,$\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2}$ と分かる。
$\theta=0$ でなくても,$\theta=\dfrac{\pi}{2}$ を代入するのもアリ。

ヒロ
もう1つは語呂合わせだ。
【語呂合わせ】
$\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}$ は「シメジ半額2-1麻衣子」と覚えよう。2年1組の麻衣子ちゃんが「シメジいかがですか~?半額ですよ~!」ってシメジを半額で売ってる様子を想像しよう。
$\sin^2$ の部分が「シメジ」,$\dfrac{\theta}{2}$ が $\theta$ の半角(はんかく)だから(訛ったのか)濁点がついて「半額(はんがく)」で左辺が終わり。右辺の「2分の1マイナスコサイン」の「2分の1」の部分が「2-1(2の1)」で「マイナスコサイン」の部分を省略して「マイコ(麻衣子)」という感じ。
こんなことを言っていたら,生徒が一言「じゃあ,コサインの方は『小さじ半額2-1プー子』ですね!」と言った。言った本人も含めてみんな意味が分からず,笑った記憶がある。つまらないことであるが,つまらないからこそ覚えている。語呂合わせなんてそんなものだ。インパクトがあって印象に残れば忘れないものである。
$\sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2}$ は「シメジ半額2-1麻衣子」と覚えよう。2年1組の麻衣子ちゃんが「シメジいかがですか~?半額ですよ~!」ってシメジを半額で売ってる様子を想像しよう。
$\sin^2$ の部分が「シメジ」,$\dfrac{\theta}{2}$ が $\theta$ の半角(はんかく)だから(訛ったのか)濁点がついて「半額(はんがく)」で左辺が終わり。右辺の「2分の1マイナスコサイン」の「2分の1」の部分が「2-1(2の1)」で「マイナスコサイン」の部分を省略して「マイコ(麻衣子)」という感じ。
こんなことを言っていたら,生徒が一言「じゃあ,コサインの方は『小さじ半額2-1プー子』ですね!」と言った。言った本人も含めてみんな意味が分からず,笑った記憶がある。つまらないことであるが,つまらないからこそ覚えている。語呂合わせなんてそんなものだ。インパクトがあって印象に残れば忘れないものである。

ヒロ
タンジェントについては,サインとコサインの符号が素早く判断できれば大丈夫だろう。

ヒロ
ここまで言っておいて言うことではないかもしれないが,「覚え方」なんてどうでも良いから,半角の公式を覚えて使いこなせるようしよう。