ここでは2直線が平行になる条件と垂直になる条件について説明します。
直線の方程式の表し方には,基本形・切片形・一般形などがあります。
どのような問題でも基本形に変形してから考えるのでは,問題を解く時間がかかったり,意図しない場合分けをする羽目になったりすることがあります。
したがって,一般形で表された2直線が平行になるときや垂直になるときの条件を,一般形のまま処理できるようにしておきましょう。
Contents
2直線の平行条件

ヒロ
まず,2直線が平行になる条件を考える。

ヒロ
基本形・切片形・一般形に分けて説明する。
基本形の2直線の平行条件

ヒロ
直線の方程式が基本形で表されているときは,すぐに傾きが分かる。

ヒロ
2つの直線の傾きが等しいときに,2直線は平行となる。
2直線の平行条件:基本形 2直線 $l,~m$ の方程式がそれぞれ $l:y=ax+b$,$m:y=cx+d$ であるとき,$l$ と $m$ が平行になるのは,2直線の傾きが等しいときである。すなわち $a=c$ のときである。さらに $b=d$ が成り立つときに,2直線は一致する。
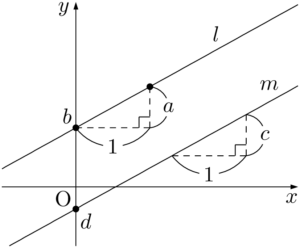

切片形の2直線の平行条件

ヒロ
切片形で表された2直線が平行になる条件を考える。

ヒロ
三角形の相似(平行線と線分の比)を考えることで,2直線が平行になる条件が分かるだろう。
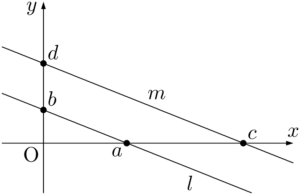
2直線の平行条件:切片形 2直線 $l,~m$ の方程式がそれぞれ $l:\dfrac{x}{a}+\dfrac{y}{b}=1$,$m:\dfrac{x}{c}+\dfrac{y}{d}=1$ であるとき,$l$ と $m$ が平行になるのは,$a:b=c:d$ が成り立つとき,すなわち $ad-bc=0$ が成り立つときである。さらに $a=c$ または $b=d$ が成り立つときに,2直線は一致する。

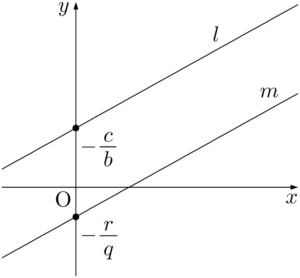
一般形の2直線の平行条件

ヒロ
一般形で表された2直線が平行になる条件を考える。

ヒロ
直線の方程式の $x$ の係数や $y$ の係数が0の場合は,座標軸に平行な直線となり,平行かどうかは簡単に分かるため,そうでない場合を考える。

ヒロ
基本形のところで言ったように,2直線の傾きが等しいとき,その2直線は平行となる。
2直線の平行条件:一般形 2直線 $l,~m$ の方程式がそれぞれ $l:ax+by+c=0$,$m:px+qy+r=0$ であるとき,$l$ と $m$ が平行になるのは,それぞれの傾き $-\dfrac{a}{b}$ と $-\dfrac{p}{q}$ が等しいときである。$-\dfrac{a}{b}=-\dfrac{p}{q}$ より,$aq-bp=0$ が成り立つときである。これは $x$ と $y$ の係数の比が等しいと捉えることもできる。その場合は $a:b=p:q$ となり,平行かどうかを調べるときは等号が成り立つかどうかに着目すれば良い。また $a:p=b:q=c:r$ が成り立つとき,2直線は一致する。


ヒロ
このことを利用すると,直線の方程式が一般形で与えられていたとしても,基本形に変形することなく,その直線と平行な直線の方程式を求めることができるようになる。
平行な直線の方程式点 $(p,~q)$ を通り,直線 $ax+by+c=0$ と平行な直線の方程式は
\begin{align*}
a(x-p)+b(y-q)=0
\end{align*}
である。a(x-p)+b(y-q)=0
\end{align*}


















