ここでは内分点と外分点の座標について説明します。
内分点・外分点とはどのような点なのかという基本から説明しているので,最後まで順番に読むことで完全に理解することができるでしょう。
最後に簡単な入試問題を解いて,計算チェックをしてみるのも良いでしょう。
Contents
数直線上の線分の内分点

ヒロ
まずは具体例から内分点について理解しよう。
【内分点とは】
例えば,数直線上の2点A(2),B(7)について,$\text{AP}:\text{PB}=3:2$ となる線分AB上の点Pを考える。点PはABを $3:2$ の比に分ける点で,ABの内側にあるから「ABを $3:2$ に内分する点」と呼ばれる。

APの長さを考えると,ABを5等分した3つ分だと分かる。つまり,$\text{AP}=\dfrac{3}{5}\text{AB}$ である。ここで,ABの長さは
\begin{align*}
\text{AB}=7-2=5
\end{align*}
であるから,\text{AB}=7-2=5
\end{align*}
\begin{align*}
\text{AP}=\dfrac{3}{5}\Cdota5=3
\end{align*}
よって,点Pの座標は\text{AP}=\dfrac{3}{5}\Cdota5=3
\end{align*}
\begin{align*}
(\text{P}の座標)&=(\text{A}の座標)+\text{AP} \\[4pt]
&=2+3=5
\end{align*}
(\text{P}の座標)&=(\text{A}の座標)+\text{AP} \\[4pt]
&=2+3=5
\end{align*}

ヒロ
このことを一般化しよう。
【ABを $m:n$ の比に内分する点P】
数直線上の2点A$(a)$,B$(b)~(a<b)$ について,ABを $m:n~(m>0,~n>0)$ の比に内分する点P$(p)$ を考える。

数直線上の2点A$(a)$,B$(b)~(a<b)$ について,ABを $m:n~(m>0,~n>0)$ の比に内分する点P$(p)$ を考える。

APの長さを求めると
\begin{align*} \text{AP}=\dfrac{m}{m+n}\text{AB}=\dfrac{m}{m+n}(b-a) \end{align*}
となるから, \begin{align*} p&=(\text{A}の座標)+\text{AP} \\[4pt] &=a+\dfrac{m}{m+n}(b-a) \\[4pt] &=\dfrac{na+mb}{m+n} \end{align*}

ヒロ
覚え方で有名なのは,次のようにクロスに掛ける方法。

ヒロ


ヒロ
詳しく言うと,分母については $m:n$ の $m$ と $n$ の和 $m+n$ を書いて,分子についてはクロスに掛けたものを足して $na+mb$ とすれば良い。

ヒロ
この方法のデメリットとしては,予め図が描かれている場合は良いが,そうでなければ,図を描くか想像しないと内分点の座標を求められなくなるかもしれないことである。

ヒロ
分母については問題ないはずだから,図を描かなくても分子を計算できるように考え方を変えよう。

ヒロ
「ABを $m:n$ の比に内分する」という文章を見て,「外側どうし,内側どうしの積の和」を考えることで,図を描かなくても内分点の座標を計算することができる。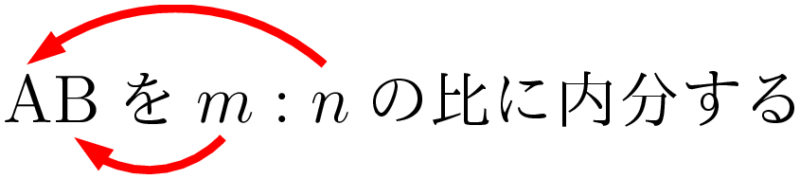

ヒロ
これで図を描かなくても,簡単に内分点の座標を求めることができるだろう。

ヒロ
上では点Aが点Bより左側にある場合を考えたが,点Aが点Bより右側にある場合も,内分点Pの座標は同じ式になる。
数直線上の線分の内分点数直線上の2点A$(a)$,B$(b)$ に対して,線分ABを $m:n$ に内分する点をPとすると,Pの座標は
\begin{align*}
\dfrac{na+mb}{m+n}
\end{align*}
となる。ただし,$m>0,~n>0$ とする。\dfrac{na+mb}{m+n}
\end{align*}


















