ここでは点の座標を求める問題について説明します。
求める点の座標を文字でおいて,与えられた条件から方程式を立てて,それを解くことで文字の値を求める方法が基本的解法です。
今回扱う問題は,それほど難しいものではありませんが,確実に解けるようにしておくことで難しい問題を解くことができるようになります。
正三角形になるための条件

ヒロ
3辺の長さが等しい三角形を正三角形というのだから,次のことが言える。
正三角形になるための条件平面上に3点が与えられたとき,その3点を結んでできる三角形が正三角形になるのは,どの2点間の距離も等しくなるときである。
点の座標を求める問題【東京電機大】
2011年 東京電機大座標平面上に3点O,A,Bがある。O$(0,~0)$,A$(-2,~-1)$ であり,点Bは第2象限にあるとする。$\sankaku{OAB}$ が正三角形であるとき,Bの座標を求めよ。
【考え方と解答】
点Bの座標をB$(x,~y)$ とおくと,$\sankaku{OAB}$ が正三角形であるとき,
点Bの座標をB$(x,~y)$ とおくと,$\sankaku{OAB}$ が正三角形であるとき,
\begin{align*}
\text{OA}^2=\text{OB}^2=\text{AB}^2
\end{align*}
が成り立つから\text{OA}^2=\text{OB}^2=\text{AB}^2
\end{align*}
\begin{align*}
&(-2)^2+(-1)^2=x^2+y^2=(x+2)^2+(y+1)^2 \\[4pt]
&\begin{cases}
x^2+y^2=5~\cdots\cdots① \\[4pt]
(x+2)^2+(y+1)^2=5~\cdots\cdots②
\end{cases}
\end{align*}
$②-①$ より&(-2)^2+(-1)^2=x^2+y^2=(x+2)^2+(y+1)^2 \\[4pt]
&\begin{cases}
x^2+y^2=5~\cdots\cdots① \\[4pt]
(x+2)^2+(y+1)^2=5~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&2(2x+2)+(2y+1)=0 \\[4pt]
&y=\dfrac{-4x-5}{2}~\cdots\cdots③
\end{align*}
ここで,点Bは第2象限にあるから&2(2x+2)+(2y+1)=0 \\[4pt]
&y=\dfrac{-4x-5}{2}~\cdots\cdots③
\end{align*}
\begin{align*}
&\dfrac{-4x-5}{2}>0 \\[4pt]
&x<-\dfrac{5}{4} \end{align*}
③を①に代入すると &\dfrac{-4x-5}{2}>0 \\[4pt]
&x<-\dfrac{5}{4} \end{align*}
\begin{align*} &x^2+\left(\dfrac{-4x-5}{2}\right)^2=5 \\[4pt] &4x^2+(4x+5)^2=20 \\[4pt] &20x^2+40x+5=0 \\[4pt] &4x^2+8x+1=0 \\[4pt] &x=\dfrac{-4\pm2\sqrt{3}}{4}=\dfrac{-2\pm\sqrt{3}}{2} \end{align*}
$x<-\dfrac{5}{4}$ より,$x=\dfrac{-2-\sqrt{3}}{2}$ このとき③より \begin{align*} y=\dfrac{-2(-2-\sqrt{3})-5}{2}=\dfrac{-1+2\sqrt{3}}{2} \end{align*}
したがって,求める点Bの座標は $\left(\dfrac{-2-\sqrt{3}}{2},~\dfrac{-1+2\sqrt{3}}{2}\right)$点の座標を求める問題【立教大】
2008年 立教大座標平面上に3点A$(-1,~-2)$,B$(1,~2)$,Cがある。点Cの $x$ 座標が正であり $\sankaku{ABC}$ が正三角形になるとき,点Cの座標は $\left(\myhako,~\myhako\right)$ である。
【考え方と解答】
上の問題と同じように考えても良いが,2点A,Bの座標をよく見ると何かに気付くだろう。このような問題で,図を描いて考える人の方が気付きやすいかもしれない。この問題では,2点A,Bは原点に関して対称になっている(中点が原点と一致している)。このことをうまく利用しよう。
$\sankaku{ABC}$ は正三角形であるから,点Cから辺ABに下ろした垂線の足は原点である。点Cの $x$ 座標は正であるから,点Cは第4象限にある。
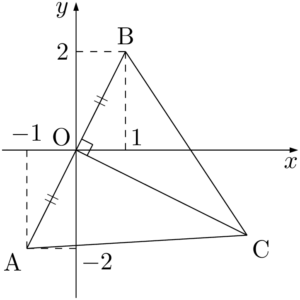
原点を通り,ABに垂直な直線の方程式は $y=-\dfrac{1}{2}x$ であるから,点Cの座標は $(2t,~-t)~(t>0)$ とおくことができる。2点A,Bについて
したがって,求める点Cの座標はC $(2\sqrt{3},~-\sqrt{3})$
上の問題と同じように考えても良いが,2点A,Bの座標をよく見ると何かに気付くだろう。このような問題で,図を描いて考える人の方が気付きやすいかもしれない。この問題では,2点A,Bは原点に関して対称になっている(中点が原点と一致している)。このことをうまく利用しよう。
$\sankaku{ABC}$ は正三角形であるから,点Cから辺ABに下ろした垂線の足は原点である。点Cの $x$ 座標は正であるから,点Cは第4象限にある。

原点を通り,ABに垂直な直線の方程式は $y=-\dfrac{1}{2}x$ であるから,点Cの座標は $(2t,~-t)~(t>0)$ とおくことができる。2点A,Bについて
\begin{align*}
\text{AB}^2=(1+1)^2+(2+2)^2=20
\end{align*}
となるから,$\text{AC}^2=20$ となる。よって\text{AB}^2=(1+1)^2+(2+2)^2=20
\end{align*}
\begin{align*}
&(2t+1)^2+(-t+2)^2=20 \\[4pt]
&5t^2=15 \\[4pt]
&t=\pm\sqrt{3}
\end{align*}
$t>0$ より,$t=\sqrt{3}$&(2t+1)^2+(-t+2)^2=20 \\[4pt]
&5t^2=15 \\[4pt]
&t=\pm\sqrt{3}
\end{align*}
したがって,求める点Cの座標はC $(2\sqrt{3},~-\sqrt{3})$