2018年センター試験 数学IA 第5問 平面図形の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
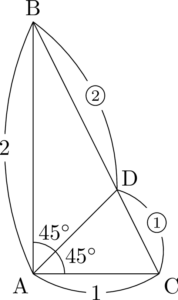
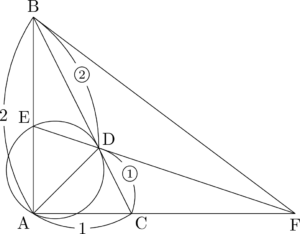
$\kaku{A}$ の二等分線と辺BCとの交点をDとすると,$\mathrm{BD}=\dfrac{\myBox{ア}\sqrt{\myBox{イ}}}{\myBox{ウ}}$ である。
点Aを通り点Dで辺BCに接する円と辺ABとの交点でAと異なるものをEとすると,$\mathrm{AB}\Cdot\mathrm{BE}=\dfrac{\myBox{エオ}}{\myBox{カ}}$ であるから,$\mathrm{BE}=\dfrac{\myBox{キク}}{\myBox{ケ}}$ である。
次の $\mybox{コ}$ には下の⓪~②から,$\mybox{サ}$ には③・④から当てはまるものを一つずつ選べ。
$\dfrac{\mathrm{BE}}{\mathrm{BD}}\myBox{コ}\dfrac{\mathrm{AB}}{\mathrm{BC}}$ であるから,直線ACと直線DEの交点は辺ACの端点 $\myBox{サ}$ の側の延長上にある。
⓪ $<$ ① $=$ ② $>$ ③ A ④ C
その交点をFとすると,$\dfrac{\mathrm{CF}}{\mathrm{AF}}=\dfrac{\myBox{シ}}{\myBox{ス}}$ であるから,$\mathrm{CF}=\dfrac{\myBox{セ}}{\myBox{ソ}}$ である。したがって,BFの長さが求まり,$\dfrac{\mathrm{CF}}{\myBox{AC}}=\dfrac{\mathrm{BF}}{\myBox{AB}}$ であることが分かる。
次の $\mybox{タ}$ には下の⓪~③から当てはまるものを一つ選べ。
点Dは $\sankaku{ABF}$ の $\myBox{タ}$。
⓪ 外心である ① 内心である ② 重心である
③ 外心,内心,重心のいずれでもない
考え方と解答

$\sankaku{ABC}$ は $1:2:\sqrt{5}$ の有名直角三角形だね。角の二等分線の性質を利用してBDを求めよう。
ADは $\kaku{A}$ の二等分線だから,
\mathrm{CD:DB}&=\mathrm{CA:AB} \\[4pt]
&=1:2
\end{align*}
$\mathrm{BC}=\sqrt{5}$ より
\mathrm{BD}=\dfrac{2}{3}\mathrm{BC}=\dfrac{2\sqrt{5}}{3}
\end{align*}

次は条件を満たすような円を描いて考えよう。すでに描いた図に円を追加して描くのは難しいけど頑張ろう。
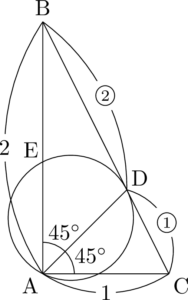
方べきの定理より
\mathrm{AB}\Cdota\mathrm{BE}&=\mathrm{BD}^2 \\[4pt]
&=\left(\dfrac{2\sqrt{5}}{3}\right)^2 \\[4pt]
&=\dfrac{20}{9}
\end{align*}

ABの長さが分かっているから,いま求めた式を利用すればBEを求めることができるね。
$\mathrm{AB}=2$ より
&2\mathrm{BE}=\dfrac{20}{9} \\[4pt]
&\mathrm{BE}=\dfrac{10}{9}
\end{align*}

次は辺の比の値を比べる問題。
\dfrac{\mathrm{BE}}{\mathrm{BD}}&=\dfrac{\dfrac{10}{9}}{\dfrac{2\sqrt{5}}{3}}=\dfrac{5}{3\sqrt{5}} \\[4pt]
\dfrac{\mathrm{AB}}{\mathrm{BC}}&=\dfrac{2}{\sqrt{5}}=\dfrac{6}{3\sqrt{5}}
\end{align*}

この結果から2直線AC, DEの交点がAとCのどちらの側の延長上にあるかを判断しなければならない。
点Dから辺ABに下ろした垂線の足をHとする。仮に $\dfrac{\mathrm{BE}}{\mathrm{BD}}=\dfrac{\mathrm{AB}}{\mathrm{BC}}$ であるとすると,点Eは点Hに一致する。
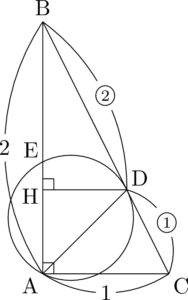
しかし,実際には $\dfrac{\mathrm{BE}}{\mathrm{BD}}<\dfrac{\mathrm{AB}}{\mathrm{BC}}$ であるから,点Eは2点B,Hの間にあることがわかる。
したがって,直線ACと直線DEの交点は辺ACの端点Cの側の延長上にある。$\myBox{サ}=④$

次はCFとAFの長さの比を求める問題。
点Fは次の図の位置にある。
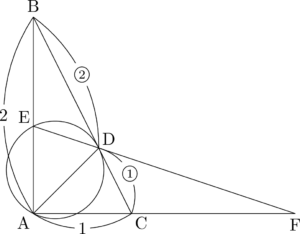
この図で $\mathrm{CF:AF}$ を求めることを考えると,メネラウスの定理を用いれば良いことが分かる。$\mathrm{BE}=\dfrac{10}{9}$ より
\mathrm{BE:EA}&=\dfrac{10}{9}:\left(2-\dfrac{10}{9}\right) \\[4pt]
&=5:4
\end{align*}
&\dfrac{\mathrm{FC}}{\mathrm{AF}}\Cdota\dfrac{\mathrm{DB}}{\mathrm{CD}}\Cdota\dfrac{\mathrm{EA}}{\mathrm{BE}}=1 \\[4pt]
&\dfrac{\mathrm{CF}}{\mathrm{AF}}\Cdota\dfrac{2}{1}\Cdota\dfrac{4}{5}=1 \\[4pt]
&\dfrac{\mathrm{CF}}{\mathrm{AF}}=\dfrac{5}{8}
\end{align*}

いま求めた等式からCFを求めよう。
$\mathrm{AF}=\mathrm{CF}+1$ であるから,$\dfrac{\mathrm{CF}}{\mathrm{AF}}=\dfrac{5}{8}$ より
&\dfrac{\mathrm{CF}}{\mathrm{CF}+1}=\dfrac{5}{8} \\[4pt]
&8\mathrm{CF}=5(\mathrm{CF}+1) \\[4pt]
&\mathrm{CF}=\dfrac{5}{3}
\end{align*}

次は点Dが $\sankaku{ABF}$ の何かを求める問題。
「$\dfrac{\mathrm{CF}}{\mathrm{AC}}=\dfrac{\mathrm{BF}}{\mathrm{AB}}$ であることがわかる」とあるが,これを確認する必要はない。仮に考えた結果,確かに成り立つということが分かったところで,問題に関する部分については何も解答が進んでいないのだから。
したがって,$\dfrac{\mathrm{CF}}{\mathrm{AC}}=\dfrac{\mathrm{BF}}{\mathrm{AB}}$ から何が分かるのかを考えよう。これは $\mathrm{CF}:\mathrm{AC}=\mathrm{BF}:\mathrm{AB}$ と考えよう。
2点B, Fを結ぶことによって,BCが $\kaku{ABF}$ の角の二等分線であることが分かる。よって,点Dは角の二等分線の交点であることが分かるから,点Dは $\sankaku{ABF}$ の内心である。$\myBox{タ}=①$

ここで三角形の内心について復習しておこう。

三角形の内心とは何かと聞かれると,「三角形の内接円の中心」と答える人が多いが,こんなのは当たり前のことで,この程度の知識では問題を解くことができない。

しっかりと,内心は3つの角の二等分線の交点だと答えられるようにしよう。

上の解答では,点Dが $\kaku{ABF}$ と $\kaku{A}$ の二等分線の交点であることを示したが,$\kaku{AFB}$ の二等分線が点Dを通ることについては触れていない。

今回の問題では,ADが $\kaku{BAF}$ の二等分線であることは最初から分かっているから,$\dfrac{\mathrm{CF}}{\mathrm{AC}}=\dfrac{\mathrm{BF}}{\mathrm{AB}}$ からBCが $\kaku{ABF}$ の二等分線であることが分かった時点で,すぐに点Dが内心であると結論付けて良い。

もう少し言うと,ADが $\kaku{BAF}$ の二等分線であるから,点Dは内心かもしれないなと,問題文を読んですぐに予想できると良いね。
2018年 センター数学IA 平面図形を解いた感想

2辺の長さが1と2であるのを見て,$1:2:\sqrt{3}$ の直角三角形と勘違いしないようにしたい。

辺の長さの積を求める問題では,最初に方べきの定理を利用することを考えよう。

2018年の問題では,内心と角の二等分線の性質について理解していれば大丈夫だね。今後のためにも,外心や垂心などについても復習しておくと良いだろう。




















