2017年センター試験 数学ⅡB 第2問微積の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
(1) 点Pを通り,放物線 $C$ に接する直線の方程式を求めよう。
$C$ 上の点 $(t,~t^2+1)$ における接線の方程式は
y=\myBox{ア}~tx-t^2+\myBox{イ}
\end{align*}
t^2-\myBox{ウ}~at+\myBox{エ}~a-\myBox{オ}=0
\end{align*}
y=\left(\myBox{コ}~a-\myBox{サ}\right)x-\myBox{シ}~a^2+\myBox{ス}~a~\cdots\cdots①
\end{align*}
y=\myBox{セ}~x
\end{align*}
(2) (1)の方程式①で表される直線を $\ell$ とする。$\ell$ と $y$ 軸との交点を $\mathrm{R}(0,~r)$ とすると,$r=-\mybox{シ}~a^2+\mybox{ス}~a$ である。$r>0$ となるのは,$\myBox{ソ}<a<\myBox{タ}$ のときであり,このとき,三角形OPRの面積 $S$ は
S=\myBox{チ}\left(\myBox{ツ}-\myBox{テ}\right)
\end{align*}
$\mybox{ソ}<a<\mybox{タ}$ のとき,$S$ の増減を調べると,$S$ は $a=\dfrac{\myBox{ト}}{\myBox{ナ}}$ で最大値 $\dfrac{\myBox{ニ}}{\myBox{ヌネ}}$ をとることがわかる。
(3) $\mybox{ソ}<a<\mybox{タ}$ のとき,放物線 $C$ と(2)の直線 $\ell$ および2直線 $x=0,~x=a$ で囲まれた図形の面積を $T$ とすると
T=\dfrac{\myBox{ノ}}{\myBox{ハ}}~a^3-\myBox{ヒ}~a^2+\myBox{フ}
\end{align*}
⓪ 減少する ① 極小値を取るが,極大値はとらない
② 増加する ③ 極大値を取るが,極小値はとらない
④ 一定である ⑤ 極小値と極大値の両方をとる
(1)の解答

放物線上の点における接線は,放物線上にない点から放物線に引いた接線を簡単に求める方法を利用して求めよう。
$y’=2x$ より,点 $(t,~t^2+1)$ における接線の方程式は
y=2tx-t^2+1
\end{align*}

次は点Pが今求めた接線上にある条件を考える問題。
点 $\mathrm{P}(a,~2a)$ が接線 $y=2tx-t^2+1$ 上にあるとき
&2a=2ta-t^2+1 \\[4pt]
&t^2-2at+2a-1=0
\end{align*}

$t$ の2次方程式を解けば良いんだけど,係数に文字が含まれることで,時間がかかる人がいるかもしれない。

方程式を解くときの基本は因数分解というのは大丈夫だろう。今は2文字あるから,次数の低い方に着目しよう。

つまり,$a$ に着目することになる。そうすると $-2at+2a$ の二項が見つかる。解を $t$ に代入したときに,これらが0になることを考えると,$t=1$ が見つかる。

実際に,$t=1$ のとき,残った二項 $t^2-1$ も0になるから,$t-1$ でくくれることが分かる。

もう1つの方は,定数項に着目することで,簡単に求めることができる。
&t^2-2at+2a-1=0 \\[4pt]
&(t-1)(t-2a+1)=0 \\[4pt]
&t=1,~2a-1
\end{align*}

次は問題文をしっかり読もう。$a\neq\myBox{ケ}$ のときに接線が2本あると言われている。

今求めたいのは,点Pを通る $C$ の接線で,$t$ の値が1つ決まったときに接線も1本決まることを理解しているかどうかがポイント。

つまり,接線が2本あるときは $t$ の値も2つないといけない。ここで「1と $2a-1$ の2つあるんじゃないの?」と思っている人は,この問題を解くことはできない。1と $2a-1$ が異なる値のときに $t$ の値が2つあると思わないといけない。
接線が2本あるのは,$2a-1\neq1$ のとき,すなわち,$a\neq1$ のときである。
$t=2a-1$ のとき,接線の方程式は
y&=2(2a-1)x-(2a-1)^2+1 \\[4pt]
&=(4a-2)x-4a^2+4a
\end{align*}
y=2x
\end{align*}
(2)の解答
(2) (1)の方程式①で表される直線を $\ell$ とする。$\ell$ と $y$ 軸との交点を $\mathrm{R}(0,~r)$ とすると,$r=-\mybox{シ}~a^2+\mybox{ス}~a$ である。$r>0$ となるのは,$\myBox{ソ}<a<\myBox{タ}$ のときであり,このとき,三角形OPRの面積 $S$ は
\begin{align*}となる。
S=\myBox{チ}\left(\myBox{ツ}-\myBox{テ}\right)
\end{align*}
$\mybox{ソ}<a<\mybox{タ}$ のとき,$S$ の増減を調べると,$S$ は $a=\dfrac{\myBox{ト}}{\myBox{ナ}}$ で最大値 $\dfrac{\myBox{ニ}}{\myBox{ヌネ}}$ をとることがわかる。

$r$ と $a$ の関係式については軽く流そう。$r>0$ を解くことを優先しよう。
$r>0$ より
&-4a^2+4a>0 \\[4pt]
&a(a-1)<0 \\[4pt]
&0<a<1
\end{align*}

次は三角形OPRの面積を求める問題。
三角形OPRは次の図のようになる。


次の最大値は3次関数の等間隔性を利用しよう。慣れれば暗算でできるようになる。
$y=2(a^2-a^3)$ は
y=-2a^2(a-1)
\end{align*}
このことと,3次関数の等間隔性を利用して,グラフを描く。まずは適当な大きさの長方形を8等分したものを書く。
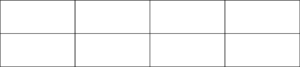
$x^3$ の係数が負だから,通る5点は次の図の黒丸になる。

次に,通るべき5点(黒丸)を通るように3次関数のグラフを描く。
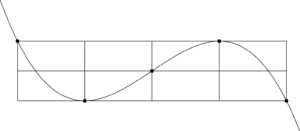
グラフが原点で $x$ 軸に接していることを考えて座標軸を描く。
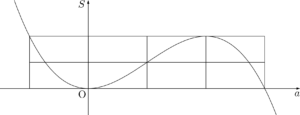
また,$S=-2a^2(a-1)$ より,グラフは点 $(1,~0)$ を通るから,分かるように「1」を追記する。
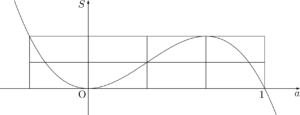
最後に,等間隔であることを利用すれば極大をとる $a$ の値が分かる。
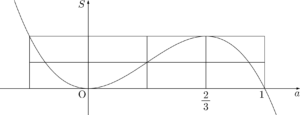
今回は $0<a<1$ の範囲を考えているから,$a=\dfrac{2}{3}$ のとき,$S$ が最大になることが分かる。

最大値については $a=\dfrac{2}{3}$ を代入しても良いし,極値の差の公式を利用しても良い。
極値の差の公式から
(最大値)&=\dfrac{1}{2}\Cdota2\Cdota\left(\dfrac{2}{3}\right)^3 \\[4pt]
&=\dfrac{8}{27}
\end{align*}
(3)の解答
(3) $\mybox{ソ}<a<\mybox{タ}$ のとき,放物線 $C$ と(2)の直線 $\ell$ および2直線 $x=0,~x=a$ で囲まれた図形の面積を $T$ とすると
\begin{align*}である。$\dfrac{\myBox{ト}}{\myBox{ナ}}\leqq a<\mybox{タ}$ の範囲において,$T$ は $\myBox{ヘ}$。$\myBox{ヘ}$ に当てはまるものを,次の⓪~⑤のうちから一つ選べ。
T=\dfrac{\myBox{ノ}}{\myBox{ハ}}~a^3-\myBox{ヒ}~a^2+\myBox{フ}
\end{align*}
⓪ 減少する ① 極小値を取るが,極大値はとらない
② 増加する ③ 極大値を取るが,極小値はとらない
④ 一定である ⑤ 極小値と極大値の両方をとる

放物線と接線と $y$ 軸で囲まれた図形の面積だから,3分の1公式を利用しよう。
$T$ は図の斜線部分の面積である。
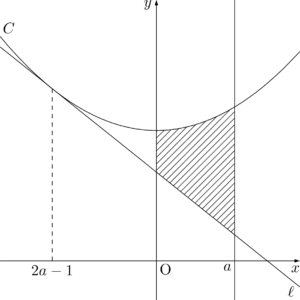
「3分の1公式の形になってないから使えない」という人は頭が固い。もっと柔軟に考えよう。次の2つの図を見れば,斜線部分の面積が青い図形の面積と緑の図形の面積の差であると理解できるはず。
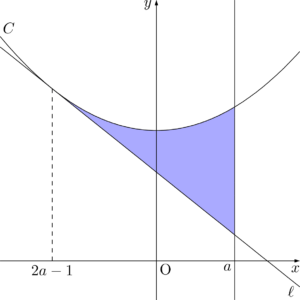

よって
T&=\dfrac{1}{3}(-a+1)^3-\dfrac{1}{3}(-2a+1)^3 \\[4pt]
&=\dfrac{1}{3}(7a^3-9a^2+3a) \\[4pt]
&=\dfrac{7}{3}a^3-3a^2+a
\end{align*}

最後は $T$ の増減と極値について言えることを考える問題。微分して考えよう。
\dfrac{dT}{da}&=7a^2-6a+1
\end{align*}
&7a^2-6a+1=0 \\[4pt]
&a=\dfrac{3\pm\sqrt{2}}{7}
\end{align*}
&\dfrac{2}{3}-\dfrac{3+\sqrt{2}}{7} \\[4pt]
&=\dfrac{5-3\sqrt{2}}{21}>0
\end{align*}
したがって,$\dfrac{2}{3}\leqq a<1$ において,$T$ は単調に増加する。$\myBox{ヘ}=②$
2017年 センター数学ⅡB微積を解いた感想

センター数学の微積では,いかに時間短縮するかが重要。

放物線上の点における接線や因数分解のちょっとしたテクニックなど,細かいテクニックが時間短縮につながる。

また,3次関数の等間隔性や極値の差の公式,3分の1公式を利用することで,かなりの時間を短縮できた。

特に面積の計算では,定積分の式を書いたり積分計算していると,それだけである程度の時間を取られてしまう。ただ,使いこなすためには,それなりの実力が必要なので,本質の理解が重要だ。




















