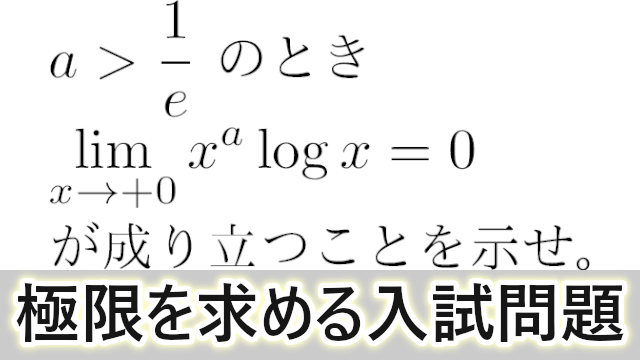極限を求める入試問題【2005年 千葉大】

大学入試問題に出題される極限に関する証明問題では「はさみうちの原理」を利用するものが多いことが知られています。

しかし「はさみうちの原理」を利用することが分かっていても，どのように利用するかが難しい問題もあります。

そういう問題こそ，合否に直結する問題で，解けなかった場合に不合格に近づいてしまうことになります。

有名問題については，解法を丸ごと覚えてしまうという方法もありますが，重要なポイントだけを覚えて細かい部分を覚えないことも大切です。

Contents

1 2005年千葉大

2005年千葉大

ヒロ

それでは次の問題を解いてみよう。

2005年千葉大以下において $\log x$ は自然対数を表す。
(1) $a>\dfrac1e$ のとき，$x>0$ に対し $x^a>\log x$ であることを示せ。
(2) $a>\dfrac1e$ のとき，$\dlim{x\to+0}x^a\log x=0$ が成り立つことを示せ。
(3) $0<t<\dfrac1e$ として，曲線 $y=x\log x~(t\leqq x\leqq1)$ および $x$ 軸と直線 $x=t$ で囲まれた部分を，$y$ 軸のまわりに回転して得られる図形の体積を $V(t)$ とする。このとき，$\dlim{t\to+0}V(t)$ を求めよ。

(1)の考え方と解答

ヒロ

(1)はグラフを利用すれば証明できるね。

ヒロ

今回の場合は $f(x)=x^a-\log x$ とおいて $x>0$ における $f(x)$ の最小値が正であることを示すんですね。

ヒロ

そうだね。解いていこう。

【(1)の解答】
$f(x)=x^a-\log x$ とおくと，

\begin{align*}
f'(x)&=ax^{a-1}-\dfrac1x \\[4pt]
&=\dfrac ax\left(x^a-\dfrac1a\right)
\end{align*}

$f'(x)=0$ とすると，

\begin{align*}
&x^a=\dfrac1a \\[4pt]
&x=\left(\dfrac1a\right)^{\frac1a}
\end{align*}

$\alpha=\left(\dfrac1a\right)^{\frac1a}$ とおくと，$f(x)$ の増減は次のようになる。

\begin{align*}
\begin{array}{|c||c|c|c|c|}\hline
x & 0 & \cdots & \alpha & \cdots \\[4pt]\hline
f'(x) & & – & 0 & + \\[4pt]\hline
f(x) & & \searrow & & \nearrow \\[4pt]\hline
\end{array}
\end{align*}

ここで

\begin{align*}
f(\alpha)&=\alpha^a-\log\alpha \\[4pt]
&=\dfrac1a+\dfrac1a\log a=\dfrac1a(1+\log a)
\end{align*}

であるから，$a>\dfrac1e$ より，$f(\alpha)>0$
したがって，$a>\dfrac1e$ のとき，$x^a>\log x$ が成り立つ。

(2)の考え方と解答

(2) $a>\dfrac1e$ のとき，$\dlim{x\to+0}x^a\log x=0$ が成り立つことを示せ。

これは(1)で不等式の証明をしているので「はさみうちの原理」を利用すれば良いはずです。

以前に $\dlim{x\to+0}x\log x=0$ を証明したので，似たような感じですね。

$0<\log x<\sqrt{x}$ の証明は省略しますね。

【(2)の解答？】
$x>0$ において，$0<\log x<\sqrt{x}$ が成り立つから，辺々を $x^a~(>0)$ で割ると

\begin{align*} 0<\dfrac{\log x}{x^a}<\dfrac{\sqrt{x}}{x^a} \end{align*}

ここで

\begin{align*} \dlim{x\to\infty}\dfrac{\sqrt{x}}{x^a} &=\dlim{x\to\infty}x^{\frac{1}{2}-a} \\[4pt] &=0 \end{align*}

であるから，はさみうちの原理より

\begin{align*} &\dlim{x\to\infty}\dfrac{\log x}{x^a}=0 \end{align*}

$x=\dfrac{1}{t}$ とおくと

\begin{align*} &\dlim{t\to+0}\dfrac{\log\dfrac{1}{t}}{\left(\dfrac{1}{t}\right)^a}=0 \\[4pt] &\dlim{t\to+0}(-t^a\log t)=0 \\[4pt] &\dlim{t\to+0}t^a\log t=0 \end{align*}

よって $\dlim{x\to+0}x^a\log x=0$

ヒロ

ちょっと適当にやってない？

【適当にやっている部分】
$\dlim{x\to\infty}x^{\frac{1}{2}-a}=0$ としているけど，仮に $a=\dfrac{1}{2}~\left(>\dfrac{1}{e}\right)$ のときは

\begin{align*}
\dlim{x\to\infty}x^{\frac{1}{2}-a}=1
\end{align*}

となるから成り立たない。

ヒロ

問題文の $a$ の条件として $a>\dfrac{1}{2}$ と与えられているなら，今の解法でも大丈夫だけど，今回はもう少し厳しい条件が与えられているから，その部分に注意しないといけないね。

確かに証明できた気でいました。これだと全然ダメですね。

でも，そのまま(1)の不等式を利用しようとしても，うまくいきませんよね？

【(1)の不等式をそのまま利用しようとしてもダメ】
$a>\dfrac{1}{e}$ のとき $x^a>\log x$ が成り立つから

\begin{align*}
0<\dfrac{\log x}{x^a}<1
\end{align*}

これだと，はさみうちの原理が使えないんですよね・・・

ヒロ

そうだね。少し工夫をしてから(1)の不等式を利用しよう。

【(1)の不等式を工夫して利用する】
いま(1)の不等式は $a>\dfrac{1}{e}$ を満たす $a$ に対して $x^a>\log x$ が成り立つというもの。
そこで $a$ を $\dfrac{1}{e}$ より大きい別のものに変えてしまおう。
その値を仮に $b$ と書くことにすると

\begin{align*} x^b>\log x \end{align*}

が成り立つ。つまり

\begin{align*} 0<\dfrac{\log x}{x^a}<x^{b-a} \end{align*}

が成り立つ。ここで $b-a<0$ になっていれば，$\dlim{x\to\infty}x^{b-a}=0$ となるから

\begin{align*} \dlim{x\to\infty}\dfrac{\log x}{x^a}=0 \end{align*}

を証明することができる。

言っていることは分かりますけど，その $b$ をどうやって決めるんですか？

ヒロ

不等式の片方の式を変えずに，もう片方の式を変える方法を身に付ければ大丈夫だね。

そんなことできるんですか？

不等式の片方の式だけ変える方法不等式 $f(a)>k$ の右辺を変えずに左辺だけを変えたい場合は，両辺に右辺と同じものを加えて2で割れば良い。

\begin{align*} &f(a)+k>2k \\[4pt] &\dfrac{1}{2}\left(f(a)+k\right)>k \end{align*}

この応用としては，右辺の $m$ 倍を両辺に加えて $m+1$ で割る方法がある。

\begin{align*} &f(a)+mk>k+mk \\[4pt] &\dfrac{1}{m+1}\left(f(a)+mk\right)>k \end{align*}

今回の場合は $a>\dfrac{1}{e}$ の両辺に $\dfrac{1}{e}$ を加えて2で割れば良いってことですね。

ヒロ

そうだね。実際にやってみよう。

【(2)の解答】
$a>\dfrac{1}{e}$ より $\dfrac{1}{2}\left(a+\dfrac{1}{e}\right)>\dfrac{1}{e}$ となるから，(1)の結果より $t>1$ に対して

\begin{align*} &t^{\frac{1}{2}\left(a+\frac{1}{e}\right)}>\log t \end{align*}

が成り立つ。両辺を $t^a(>0)$ で割ると

\begin{align*} 0<\dfrac{\log t}{t^a}<t^{\frac{1}{2}\left(\frac{1}{e}-a\right)} \end{align*}

となる。ここで $\dfrac{1}{e}-a<0$ より

\begin{align*} \dlim{t\to\infty}t^{\frac{1}{2}\left(\frac{1}{e}-a\right)}=0 \end{align*}

となるから，はさみうちの原理より

\begin{align*} \dlim{t\to\infty}\dfrac{\log t}{t^a}=0 \end{align*}

したがって $\dfrac{1}{t}=x$ とおくと，$t\to\infty$ のとき $x\to+0$ であるから

\begin{align*} &\dlim{x\to+0}\dfrac{\log\dfrac{1}{x}}{\left(\dfrac{1}{x}\right)^a}=0 \\[4pt] &\dlim{x\to+0}x^a\log x=0 \end{align*}

(3)の考え方と解答

(3) $0<t<\dfrac1e$ として，曲線 $y=x\log x~(t\leqq x\leqq1)$ および $x$ 軸と直線 $x=t$ で囲まれた部分を，$y$ 軸のまわりに回転して得られる図形の体積を $V(t)$ とする。このとき，$\dlim{t\to+0}V(t)$ を求めよ。

ヒロ

次は回転体の体積の極限を求める問題だね。

積分するだけですね。

【(3)の解答】
$y=x\log x$ より，$y’=\log x+1$
$y’=0$ とすると，

\begin{align*}
&\log x=-1 \\[4pt]
&x=\dfrac{1}{e}
\end{align*}

よって，$y$ の増減は次のようになる。

\begin{align*}
\begin{array}{|c||c|c|c|c|}\hline
x & 0 & \cdots & \dfrac1e & \cdots \\\hline
y’ & & – & 0 & + \\\hline
y & & \searrow & -\dfrac1e & \nearrow \\\hline
\end{array}
\end{align*}

したがって，$y=x\log x$ のグラフは図のようになる。

$y=x\log x$ の $0<x\leqq\dfrac1e$ の部分を $y=x_1\log x_1$， $\dfrac1e\leqq x$ の部分を $y=x_2\log x_2$ とおくと，

\begin{align*} V(t)&=\dint{-\frac1e}{0}\pi {x_2}^2\,dy-\dint{-\frac1e}{t\log t}\pi{x_1}^2\,dy -\pi t^2\cdot(-t\log t) \\[1mm] &=\pi\dint{\frac1e}{1}x^2(\log x+1)\,dx -\pi\dint{\frac1e}{t}x^2(\log x+1)\,dx+\pi t^3\log t \\[1mm] &=\pi\dint{t}{1}x^2(\log x+1)\,dx+\pi t^3\log t \\[1mm] &=\pi\Tint{\dfrac13x^3\log x+\dfrac29x^3}{t}{1}+\pi t^3\log t \\[1mm] &=\pi\left(\dfrac29+\dfrac23t^3\log t-\dfrac29t^3\right) \end{align*}

(2)より，$\dlim{t\to+0}t^3\log t=0$だから，

\begin{align*} \dlim{t\to+0}V(t)=\dfrac29\pi \end{align*}

2005年 千葉大

(1)の考え方と解答

(2)の考え方と解答

(3)の考え方と解答

2005年千葉大