数学Ⅱで学習する12分の1公式について説明します。12分の1公式は,センター数学で面積を求める公式として知られています。
12分の1公式は裏技公式みたいに扱われることがあります。しかし,公式が成り立つ理由を知ることで,12分の1公式が当たり前に成り立つ面積公式だということに納得いくはずです。
放物線とその2本の接線で囲まれる図形の面積を求める公式が12分の1公式と呼ばれています。この公式を使うことで,途中式を書かなくて良いマーク式試験においては,かなり楽に速く面積を求めることができるようになります。
中には12分の1公式を使うのが怖くて,結局普通に積分してやってしまうという人がいますが,使い方をマスターすることで,12分の1公式を使える問題に対して強くなるでしょう。また,放物線とそれに接する2直線が囲む部分の面積を求める問題は頻出問題であり,速く解くことも重要視するなら,絶対に覚えておきたい公式の1つとなります。
2011年センター試験数学ⅡBの問題を扱って説明します。
曲線 $C$ 上の点Pの $x$ 座標を $a$ とする。点Pにおける $C$ の接線 $\ell$ の方程式は
y=\myBox{アイ}\,x-a^{\,\myBox{ウ}}
\end{align*}
\left(\dfrac{\myBox{エ}}{\myBox{オ}},~\myBox{カ}\right)
\end{align*}
$a>0$ のとき,曲線 $C$ と直線 $\ell$ および $x$ 軸で囲まれた図形の面積を $S$
とすると
S=\dfrac{a^{\,\myBox{キ}}}{\myBox{クケ}}
\end{align*}
プリントを次のリンクからダウンロードできます。
Contents
定積分で面積を求める解法(通常解法)

接線 $\ell$ の方程式を求めよう。
&y=2a(x-a)+a^2 \\[4pt]
&y=2ax-a^2
\end{align*}

次に点Qの座標を求めよう。
&2ax-a^2=0 \\[4pt]
&2a\left(x-\dfrac{a}{2}\right)=0
\end{align*}

次は面積を求める問題だから,図を描こう。
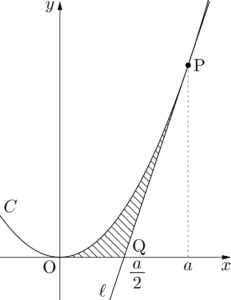
S&=\dint{0}{\frac{a}{2}}x^2\;dx+\dint{\frac{a}{2}}{a}\{x^2-(2ax-a^2)\}\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}x^3}{0}{\frac{a}{2}}+\Tint{\dfrac{1}{3}(x-a)^3}{\frac{a}{2}}{a} \\[4pt]
&=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3+\dfrac{1}{3}\left(-\dfrac{a}{2}\right)^3 \\[4pt]
&=\dfrac{a^3}{12}
\end{align*}
放物線と2本の接線で囲まれる図形の面積を一般的に求める

一般的に考えてみよう。
(1) 2直線 $\ell,~m$ の方程式を求めよ。
(2) 2直線 $\ell,~m$ の交点Rの座標を求めよ。
(3) 放物線 $C$ と2直線 $\ell,~m$ で囲まれる部分の面積 $S$ を求めよ。

(1)は微分を利用して,接線の方程式を求めよう。
$f(x)=ax^2+bx+c$ より
f'(x)=2ax+b
\end{align*}
&y=(2ap+b)(x-p)+ap^2+bp+c \\[4pt]
&y=(2ap+b)x-ap^2+c~\cdots\cdots ①
\end{align*}
y=(2aq+b)x-aq^2+c~\cdots\cdots ②
\end{align*}

(2)は連立方程式を解くだけ。
①,②より $y$ を消去すると
&2a(p-q)x-a(p^2-q^2)=0 \\[4pt]
&2a(p-q)\left(x-\dfrac{p+q}{2}\right)=0
\end{align*}
$y$ 座標 $R_y$ は
R_y&=(2ap+b)\Cdota\dfrac{p+q}{2}-ap^2+c \\[4pt]
&=apq+b\Cdota\dfrac{p+q}{2}+c
\end{align*}
\mathrm{R}\left(\dfrac{p+q}{2},~apq+b\Cdota\dfrac{p+q}{2}+c\right)
\end{align*}

3点P, Q, Rの $x$ 座標は等差数列をなす。放物線 $C$ の方程式が $y=ax^2$ のとき,点Rの座標は $\left(\dfrac{p+q}{2},~apq\right)$ になることは有名だから覚えておくと良いだろう。

今回のように $y=ax^2+bx+c$ になったとき,点Rの $x$ 座標は変わらないが,$y$ 座標は $bx+c$ だけずれる。

(3)の面積 $S$ を求めるために図を描こう。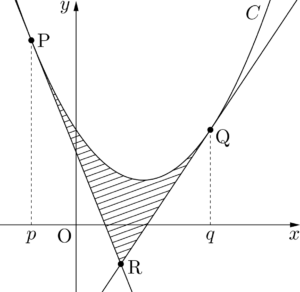

点Rを通り,$y$ 軸に平行な直線で分割して考えると,それぞれで3分の1公式が使えることが分かる。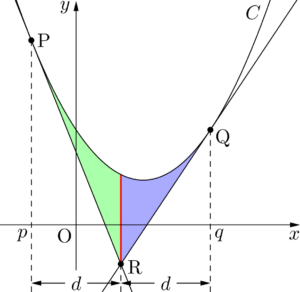

図の $d$ が $d=\dfrac{q-p}{2}$ であることと3分の1公式を使って面積 $S$ を求めよう。ただ,一応積分の式だけは書いておく。
求める面積 $S$ は
S&=\dint{p}{\frac{p+q}{2}}a(x-p)^2\;dx+\dint{\frac{p+q}{2}}{q}a(x-q)^2\;dx \\[4pt]
&=\dfrac{1}{3}a\left(\dfrac{q-p}{2}\right)^3\times2 \\[4pt]
&=\dfrac{a}{12}(q-p)^3
\end{align*}

これが12分の1公式と呼ばれるものだけど,このように,左側と右側のそれぞれに対して3分の1公式を適用することで導くことができる。
面積を求める12分の1公式

面積を求める12分の1公式を使えるようにしよう。
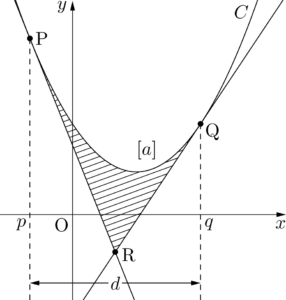
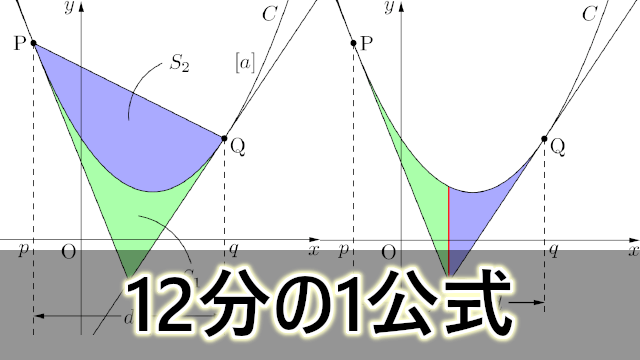
放物線 $C$ と $C$ 上の異なる2点にP, Qにおける接線で囲まれた図形の面積 $S$ は,次のように表すことができる。図中の $[a]$ は $x^2$ の係数を表し,$d$ は2点P, Qの $x$ 座標の差を表す。
S=\dfrac{\abs{a}}{12}d^3
\end{align*}
12分の1公式を利用して面積を求める
座標平面上で,放物線 $y=x^2$ を $C$ とする。
曲線 $C$ 上の点Pの $x$ 座標を $a$ とする。点Pにおける $C$ の接線 $\ell$ の方程式は\begin{align*}である。$a\neq0$ のとき直線 $\ell$ が $x$ 軸と交わる点をQとすると,Qの座標は
y=\myBox{アイ}\,x-a^{\,\myBox{ウ}}
\end{align*}\begin{align*}である。
\left(\dfrac{\myBox{エ}}{\myBox{オ}},~\myBox{カ}\right)
\end{align*}
$a>0$ のとき,曲線 $C$ と直線 $\ell$ および $x$ 軸で囲まれた図形の面積を $S$
とすると\begin{align*}である。
S=\dfrac{a^{\,\myBox{キ}}}{\myBox{クケ}}
\end{align*}

知識を利用して空欄を埋める場合,簡単に求めることができる。点Pにおける接線の方程式については,とりあえず通常の方法で求めよう。

$y=ax^2$ で表される放物線の接線を考えるときは,$x$ 軸が原点における接線であることに注意しておこう。

この意識があれば,$C$ 上の点Pにおける接線と $x$ 軸の交点Qの $x$ 座標は $\dfrac{a}{2}$ であることが計算しなくても分かる。Qの $y$ 座標は当然0だから,Qの座標は $\left(\dfrac{a}{2},~0\right)$ となる。

また,面積 $S$ は12分の1公式を利用しよう。$x^2$ の係数は1で,幅 $d$ は $a$ だから,$S=\dfrac{a^3}{12}$ となる。
放物線と2本の接線で囲まれる図形の面積比

さっきまでの $S$ を $S_1$ として,2点P, Qを結んで線分PQと放物線 $C$ で囲まれた図形の面積を $S_2$ とする。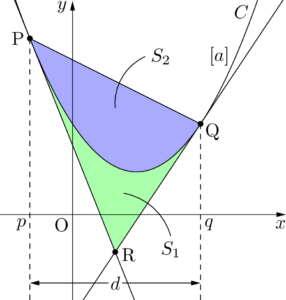
S_1=\dfrac{\abs{a}}{12}d^3
\end{align*}
S_2=\dfrac{\abs{a}}{6}d^3
\end{align*}
S_1:S_2=1:2
\end{align*}

$S_1:S_2=1:2$ になることは有名で,これを証明させる入試問題もあるので,個別試験で数学が必要な人は,自分で証明できるようにしておこう。
まとめ

面積を求める12分の1公式を適切に使うことによって,圧倒的に楽に速く面積を求めることができる。


面積を求める12分の1公式は,この記事で説明したもの以外に,3次関数に関連したものもある。知らない人は次の記事を読んで,知識を手に入れよう!