ここでは鈍角の三角比の値について説明します。
鋭角の三角比の値の考え方では鈍角の三角比の値を定めることができないため,鈍角でも三角比の値を考えることができるように考え方を変えます。
三角比の定義を知って,柔軟に対応できるようにしよう。
三角比の拡張

ヒロ
鈍角の三角比の値を考えることができるように定義を変える。
【三角比の定義】
単位円周上の点で,$x$ 軸の正の方向とのなす角が $\theta$ となる点を $\text{P}(x,~y)$ とするとき
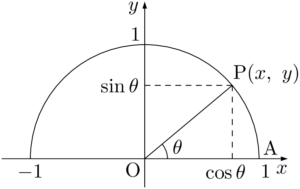
単位円周上の点で,$x$ 軸の正の方向とのなす角が $\theta$ となる点を $\text{P}(x,~y)$ とするとき
\begin{align*}
\sin\theta=y,~\cos\theta=x,~\tan\theta=\dfrac{y}{x}
\end{align*}
と定める。\sin\theta=y,~\cos\theta=x,~\tan\theta=\dfrac{y}{x}
\end{align*}


ヒロ
単位円周上の点の $x$ 座標がコサイン,$y$ 座標がサイン,原点と結んだ線分の傾きがタンジェントってことだね。

ヒロ
$\sin\theta,~\cos\theta$ の定義については,1999年の東京大の入試でも出題されている。

ヒロ
しっかりと答えられるようにしておこう。
120°の三角比の値

ヒロ
それでは120°の三角比の値を求めてみよう。
【120°の三角比の値】
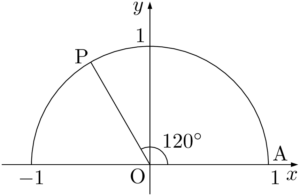
単位円周上の点で $\theta=120\Deg$ となる点をとる。
点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=60\Deg$ となるから,$\sankaku{POH}$ は $1:2:\sqrt{3}$ の直角三角形である。
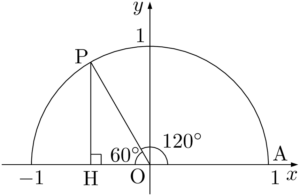
$\text{OH}:\text{OP}:\text{PH}=1:2:\sqrt{3}$ であり,$\text{OP}=1$ であるから
したがって
単位円周上の点で $\theta=120\Deg$ となる点をとる。

点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=60\Deg$ となるから,$\sankaku{POH}$ は $1:2:\sqrt{3}$ の直角三角形である。

$\text{OH}:\text{OP}:\text{PH}=1:2:\sqrt{3}$ であり,$\text{OP}=1$ であるから
\begin{align*}
\text{OH}=\dfrac{1}{2},~\text{PH}=\dfrac{\sqrt{3}}{2}
\end{align*}
となる。また,OPの傾きは $-\sqrt{3}$ である。\text{OH}=\dfrac{1}{2},~\text{PH}=\dfrac{\sqrt{3}}{2}
\end{align*}
したがって
\begin{align*}
&\sin120\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]
&\cos120\Deg=-\dfrac{1}{2} \\[4pt]
&\tan120\Deg=-\sqrt{3}
\end{align*}
&\sin120\Deg=\dfrac{\sqrt{3}}{2} \\[4pt]
&\cos120\Deg=-\dfrac{1}{2} \\[4pt]
&\tan120\Deg=-\sqrt{3}
\end{align*}
135°の三角比の値

ヒロ
同じようにして135°の三角比の値を求めよう。
【135°の三角比の値】
単位円周上の点で $\theta=135\Deg$ となる点をとる。
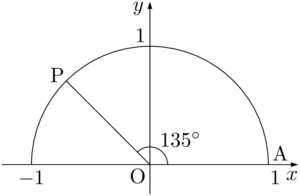
点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=45\Deg$ となるから,$\sankaku{POH}$ は $1:1:\sqrt{2}$ の直角三角形である。
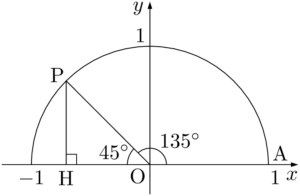
$\text{OH}:\text{PH}:\text{OP}=1:1:\sqrt{2}$ であり,$\text{OP}=1$ であるから
したがって
単位円周上の点で $\theta=135\Deg$ となる点をとる。

点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=45\Deg$ となるから,$\sankaku{POH}$ は $1:1:\sqrt{2}$ の直角三角形である。

$\text{OH}:\text{PH}:\text{OP}=1:1:\sqrt{2}$ であり,$\text{OP}=1$ であるから
\begin{align*}
\text{OH}=\dfrac{1}{\sqrt{2}},~\text{PH}=\dfrac{1}{\sqrt{2}}
\end{align*}
となる。また,OPの傾きは $-1$ である。\text{OH}=\dfrac{1}{\sqrt{2}},~\text{PH}=\dfrac{1}{\sqrt{2}}
\end{align*}
したがって
\begin{align*}
&\sin135\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]
&\cos135\Deg=-\dfrac{1}{\sqrt{2}} \\[4pt]
&\tan135\Deg=-1
\end{align*}
&\sin135\Deg=\dfrac{1}{\sqrt{2}} \\[4pt]
&\cos135\Deg=-\dfrac{1}{\sqrt{2}} \\[4pt]
&\tan135\Deg=-1
\end{align*}
150°の三角比の値

ヒロ
同じようにして150°の三角比の値を求めよう。
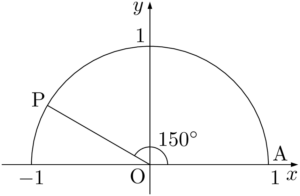
【150°の三角比の値】
単位円周上の点で $\theta=150\Deg$ となる点をとる。
点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=30\Deg$ となるから,$\sankaku{POH}$ は $1:2:\sqrt{3}$ の直角三角形である。
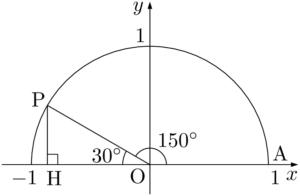
$\text{PH}:\text{OP}:\text{OH}=1:2:\sqrt{3}$ であり,$\text{OP}=1$ であるから
したがって
単位円周上の点で $\theta=150\Deg$ となる点をとる。

点Pから $x$ 軸に垂線PHを下ろすと $\kaku{POH}=30\Deg$ となるから,$\sankaku{POH}$ は $1:2:\sqrt{3}$ の直角三角形である。

$\text{PH}:\text{OP}:\text{OH}=1:2:\sqrt{3}$ であり,$\text{OP}=1$ であるから
\begin{align*}
\text{OH}=\dfrac{\sqrt{3}}{2},~\text{PH}=\dfrac{1}{2}
\end{align*}
となる。また,OPの傾きは $-\sqrt{3}$ である。\text{OH}=\dfrac{\sqrt{3}}{2},~\text{PH}=\dfrac{1}{2}
\end{align*}
したがって
\begin{align*}
&\sin150\Deg=\dfrac{1}{2} \\[4pt]
&\cos150\Deg=-\dfrac{\sqrt{3}}{2} \\[4pt]
&\tan150\Deg=-\dfrac{1}{\sqrt{3}}
\end{align*}
&\sin150\Deg=\dfrac{1}{2} \\[4pt]
&\cos150\Deg=-\dfrac{\sqrt{3}}{2} \\[4pt]
&\tan150\Deg=-\dfrac{1}{\sqrt{3}}
\end{align*}
0°,90°,180°の三角比

ヒロ
三角比の値を単位円周上の点の座標として捉えることで,0°・90°・180°の三角比の値を考えることができるようになる。
【0°,90°,180°の三角比の値】
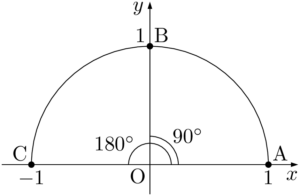
0°の三角比の値は点Aの座標とOAの傾きから,次のようになる。

0°の三角比の値は点Aの座標とOAの傾きから,次のようになる。
\begin{align*}
&\sin0\Deg=0 \\[4pt]
&\cos0\Deg=1 \\[4pt]
&\tan0\Deg=0
\end{align*}
90°の三角比の値でタンジェントだけは定義されない。それはOBの傾きが定義されないから。よって,90°の三角比の値は,点Bの座標から次のようになる。&\sin0\Deg=0 \\[4pt]
&\cos0\Deg=1 \\[4pt]
&\tan0\Deg=0
\end{align*}
\begin{align*}
&\sin90\Deg=1 \\[4pt]
&\cos90\Deg=0 \\[4pt]
&\tan90\Deg~は定義されない
\end{align*}
180°の三角比の値は点Cの座標とOCの傾きから,次のようになる。&\sin90\Deg=1 \\[4pt]
&\cos90\Deg=0 \\[4pt]
&\tan90\Deg~は定義されない
\end{align*}
\begin{align*}
&\sin180\Deg=0 \\[4pt]
&\cos180\Deg=-1 \\[4pt]
&\tan180\Deg=0
\end{align*}
&\sin180\Deg=0 \\[4pt]
&\cos180\Deg=-1 \\[4pt]
&\tan180\Deg=0
\end{align*}
三角比の拡張のまとめ

ヒロ
単位円周上の点の座標を考えることで鋭角以外の角度の三角比の値を考えることができるようになった。

ヒロ
今回求めた三角比の値をまとめると次のようになる。
いろいろな三角比の値
- $\sin0\Deg=0$
- $\cos0\Deg=1$
- $\tan0\Deg=0$
- $\sin90\Deg=1$
- $\cos90\Deg=0$
- $\tan90\Deg$ は定義されない
- $\sin120\Deg=\dfrac{\sqrt{3}}{2}$
- $\cos120\Deg=-\dfrac{1}{2}$
- $\tan120\Deg=-\sqrt{3}$
- $\sin135\Deg=\dfrac{1}{\sqrt{2}}$
- $\cos135\Deg=-\dfrac{1}{\sqrt{2}}$
- $\tan135\Deg=-1$
- $\sin150\Deg=\dfrac{1}{2}$
- $\cos150\Deg=-\dfrac{\sqrt{3}}{2}$
- $\tan150\Deg=-\dfrac{1}{\sqrt{3}}$
- $\sin180\Deg=0$
- $\cos180\Deg=-1$
- $\tan180\Deg=0$




















