Contents
2つの円の交点の座標【自治医科大】
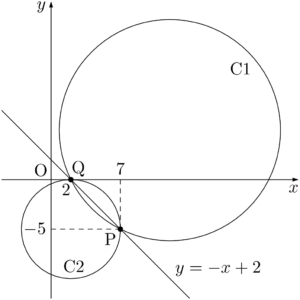
2011年 自治医科大2つの円C1 $:x^2+y^2-24x-10y+44=0$,C2 $:x^2+y^2-4x+10y+4=0$ について考える。C1とC2の相異なる2つの交点をP,Qとする。線分PQの長さをLとしたとき,$\dfrac{\text{L}^2}{10}$ の値を求めよ。
【考え方と解答】
\begin{align*}
&x^2+y^2-24x-10y+44=0~\cdots\cdots① \\[4pt]
&x^2+y^2-4x+10y+4=0~\cdots\cdots②
\end{align*}
とする。$②-①$ より&x^2+y^2-24x-10y+44=0~\cdots\cdots① \\[4pt]
&x^2+y^2-4x+10y+4=0~\cdots\cdots②
\end{align*}
\begin{align*}
&20x+20y-40=0 \\[4pt]
&y=-x+2~\cdots\cdots③
\end{align*}
③を②に代入すると&20x+20y-40=0 \\[4pt]
&y=-x+2~\cdots\cdots③
\end{align*}
\begin{align*}
&x^2+(-x+2)^2-4x+10(-x+2)+4=0 \\[4pt]
&2x^2-18x+28=0 \\[4pt]
&x^2-9x+14=0 \\[4pt]
&(x-2)(x-7)=0 \\[4pt]
&x=2,~7
\end{align*}
直線③の傾きが $-1$ であるから,&x^2+(-x+2)^2-4x+10(-x+2)+4=0 \\[4pt]
&2x^2-18x+28=0 \\[4pt]
&x^2-9x+14=0 \\[4pt]
&(x-2)(x-7)=0 \\[4pt]
&x=2,~7
\end{align*}
\begin{align*}
\text{L}&=\text{PQ} \\[4pt]
&=\sqrt{2}(7-2)=5\sqrt{2}
\end{align*}
したがって,\text{L}&=\text{PQ} \\[4pt]
&=\sqrt{2}(7-2)=5\sqrt{2}
\end{align*}
\begin{align*}
\dfrac{\text{L}^2}{10}=\dfrac{(5\sqrt{2})^2}{10}=5
\end{align*}
\dfrac{\text{L}^2}{10}=\dfrac{(5\sqrt{2})^2}{10}=5
\end{align*}


ヒロ
一般的に,平面上の2点間の距離を求めたいときは,2点の $x$ 座標と $y$ 座標を求めてから,三平方の定理を利用して2点間の距離を求めることが多い。

ヒロ
しかし,上の解答のように,2点の $x$ 座標と2点を通る直線の傾きから,2点間の距離を求めることもできる。

ヒロ
このことについては,次の記事で説明している。
2つの円の接点の座標【駒澤大】
2016年 駒澤大$a$ を定数として,次の方程式によって表される2つの円について考える。
(2) $C_1$ と $C_2$ が内接するのは $a=\myBox{オ}+2\sqrt{\myBox{カ}}$ のときであり,その接点の座標は
\begin{align*}
&C_1:(x-1)^2+(y-1)^2=a \\[4pt]
&C_2:x^2+y^2-4x-4y+7=0
\end{align*}
(1) $C_1$ と $C_2$ が外接するのは $a=\myBox{ア}-2\sqrt{\myBox{イ}}$ のときであり,その接点の座標は&C_1:(x-1)^2+(y-1)^2=a \\[4pt]
&C_2:x^2+y^2-4x-4y+7=0
\end{align*}
\begin{align*}
\left(\dfrac{\myBox{ウ}-\sqrt{\myBox{エ}}}{2},~\dfrac{\mybox{ウ}-\sqrt{\mybox{エ}}}{2}\right)
\end{align*}
である。\left(\dfrac{\myBox{ウ}-\sqrt{\myBox{エ}}}{2},~\dfrac{\mybox{ウ}-\sqrt{\mybox{エ}}}{2}\right)
\end{align*}
(2) $C_1$ と $C_2$ が内接するのは $a=\myBox{オ}+2\sqrt{\myBox{カ}}$ のときであり,その接点の座標は
\begin{align*}
\left(\dfrac{\myBox{キ}+\sqrt{\myBox{ク}}}{2},~\dfrac{\mybox{キ}+\sqrt{\mybox{ク}}}{2}\right)
\end{align*}
である。\left(\dfrac{\myBox{キ}+\sqrt{\myBox{ク}}}{2},~\dfrac{\mybox{キ}+\sqrt{\mybox{ク}}}{2}\right)
\end{align*}
【(1)の考え方と解答】
円 $C_1$ は点C $(1,~1)$ を中心とし,半径 $\sqrt{a}$ の円である。また $x^2+y^2-4x-4y+7=0$ より
また,2つの円の中心間の距離を $d$ とすると
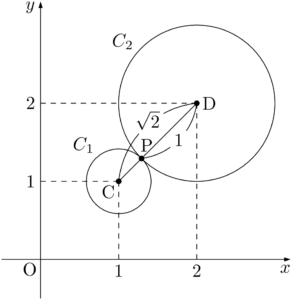
直線CDの方程式は $y=x$ であるから,点Pの座標は $(p,~p)$ と表せる。接点Pは線分CDを $(\sqrt{2}-1):1$ に内分する点であるから
円 $C_1$ は点C $(1,~1)$ を中心とし,半径 $\sqrt{a}$ の円である。また $x^2+y^2-4x-4y+7=0$ より
\begin{align*}
(x-2)^2+(y-2)^2=1
\end{align*}
となるから,円 $C_2$ は点D $(2,~2)$ を中心とし,半径1の円である。(x-2)^2+(y-2)^2=1
\end{align*}
また,2つの円の中心間の距離を $d$ とすると
\begin{align*}
d&=\sqrt{(2-1)^2+(2-1)^2}=\sqrt{2}
\end{align*}
$C_1$ と $C_2$ が外接するのは,中心間の距離が半径の和と等しいときであるからd&=\sqrt{(2-1)^2+(2-1)^2}=\sqrt{2}
\end{align*}
\begin{align*}
&\sqrt{a}+1=\sqrt{2} \\[4pt]
&\sqrt{a}=\sqrt{2}-1 \\[4pt]
&a=(\sqrt{2}-1)^2 \\[4pt]
&a=3-2\sqrt{2}
\end{align*}
&\sqrt{a}+1=\sqrt{2} \\[4pt]
&\sqrt{a}=\sqrt{2}-1 \\[4pt]
&a=(\sqrt{2}-1)^2 \\[4pt]
&a=3-2\sqrt{2}
\end{align*}

直線CDの方程式は $y=x$ であるから,点Pの座標は $(p,~p)$ と表せる。接点Pは線分CDを $(\sqrt{2}-1):1$ に内分する点であるから
\begin{align*}
p&=\dfrac{1\Cdot1+(\sqrt{2}-1)\Cdot2}{(\sqrt{2}-1)+1} \\[4pt]
&=\dfrac{2\sqrt{2}-1}{\sqrt{2}} \\[4pt]
&=\dfrac{4-\sqrt{2}}{2}
\end{align*}
よって,接点の座標はp&=\dfrac{1\Cdot1+(\sqrt{2}-1)\Cdot2}{(\sqrt{2}-1)+1} \\[4pt]
&=\dfrac{2\sqrt{2}-1}{\sqrt{2}} \\[4pt]
&=\dfrac{4-\sqrt{2}}{2}
\end{align*}
\begin{align*}
\left(\dfrac{4-\sqrt{2}}{2},~\dfrac{4-\sqrt{2}}{2}\right)
\end{align*}
\left(\dfrac{4-\sqrt{2}}{2},~\dfrac{4-\sqrt{2}}{2}\right)
\end{align*}
(2) $C_1$ と $C_2$ が内接するのは $a=\myBox{オ}+2\sqrt{\myBox{カ}}$ のときであり,その接点の座標は
\begin{align*}である。
\left(\dfrac{\myBox{キ}+\sqrt{\myBox{ク}}}{2},~\dfrac{\mybox{キ}+\sqrt{\mybox{ク}}}{2}\right)
\end{align*}
【(2)の考え方と解答】
2つの円が内接するのは,中心間の距離が半径の差に等しいときであるから
両辺を2乗して
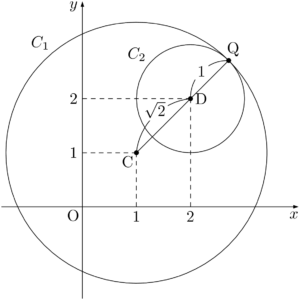
接点をQとすると,点Qは線分CDを $(\sqrt{2}+1):1$ に外分する点である。点Qの座標を $(q,~q)$ とおくと
2つの円が内接するのは,中心間の距離が半径の差に等しいときであるから
\begin{align*}
&\abs{\sqrt{a}-1}=\sqrt{2} \\[4pt]
&\sqrt{a}-1=\pm\sqrt{2} \\[4pt]
&\sqrt{a}=1\pm\sqrt{2}
\end{align*}
$\sqrt{a}>0$ より,$\sqrt{a}=1+\sqrt{2}$&\abs{\sqrt{a}-1}=\sqrt{2} \\[4pt]
&\sqrt{a}-1=\pm\sqrt{2} \\[4pt]
&\sqrt{a}=1\pm\sqrt{2}
\end{align*}
両辺を2乗して
\begin{align*}
a&=(1+\sqrt{2})^2 \\[4pt]
&=3+2\sqrt{2}
\end{align*}
a&=(1+\sqrt{2})^2 \\[4pt]
&=3+2\sqrt{2}
\end{align*}

接点をQとすると,点Qは線分CDを $(\sqrt{2}+1):1$ に外分する点である。点Qの座標を $(q,~q)$ とおくと
\begin{align*}
q&=\dfrac{-1\Cdot1+(\sqrt{2}+1)\Cdot2}{(\sqrt{2}+1)-1} \\[4pt]
&=\dfrac{2\sqrt{2}+1}{\sqrt{2}} \\[4pt]
&=\dfrac{4+\sqrt{2}}{2}
\end{align*}
よって,接点の座標はq&=\dfrac{-1\Cdot1+(\sqrt{2}+1)\Cdot2}{(\sqrt{2}+1)-1} \\[4pt]
&=\dfrac{2\sqrt{2}+1}{\sqrt{2}} \\[4pt]
&=\dfrac{4+\sqrt{2}}{2}
\end{align*}
\begin{align*}
\left(\dfrac{4+\sqrt{2}}{2},~\dfrac{4+\sqrt{2}}{2}\right)
\end{align*}
\left(\dfrac{4+\sqrt{2}}{2},~\dfrac{4+\sqrt{2}}{2}\right)
\end{align*}



















