中学校では「2乗に比例する関数」として,2次関数の基本を学習しました。
高校では2乗に比例する関数だけでなく,一般的な2次関数について学習します。
2次関数のグラフの描き方や性質などを知ることで,関数の基礎を身に付けましょう。
Contents
2次関数とは

ヒロ
2次関数は次のように定義される。
2次関数$x$ の2次式で表される関数を,$x$ の2次関数という。一般的に実数 $a,~b,~c~(a\neq0)$ を用いて
\begin{align*}
y=ax^2+bx+c
\end{align*}
と表される。y=ax^2+bx+c
\end{align*}
$y=ax^2$ のグラフ

ヒロ
$y=ax^2$ のグラフについて復習しておこう。
$y=ax^2$ のグラフ①$y=\dfrac{1}{2}x^2$, ②$y=-\dfrac{2}{3}x^2$, ③$y=2x^2$, ④$y=-\dfrac{1}{3}x^2$ のグラフはそれぞれ次のような曲線になる。
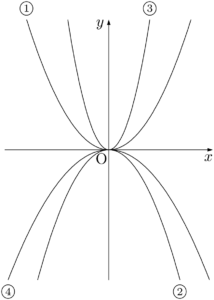
一般に,2次関数 $y=ax^2~(a\neq0)$ のグラフは原点Oを通り,$y$ 軸に関して対称な曲線であり,その曲線は放物線と呼ばれる。
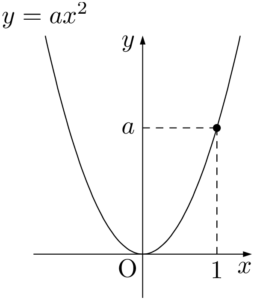
また,放物線は対称な軸をもっており,この対称の軸をその放物線の軸といい,軸と放物線の交点をその放物線の頂点という。
つまり,$y=ax^2$ のグラフは軸が $y$ 軸で,頂点が原点の放物線である。
$a>0$ のとき,$x$ の値が増加すると $x\leq0$ の範囲で $y$ の値は減少し,$x\geq0$ の範囲で $y$ の値は増加する。
$a<0$ のとき,$x$ の値が増加すると $x\leq0$ の範囲で $y$ の値は増加し,$x\geq0$ の範囲で $y$ の値は減少する。
グラフの形状から,$a>0$ のとき,下に凸,$a<0$ のとき,上に凸であるという。

一般に,2次関数 $y=ax^2~(a\neq0)$ のグラフは原点Oを通り,$y$ 軸に関して対称な曲線であり,その曲線は放物線と呼ばれる。

また,放物線は対称な軸をもっており,この対称の軸をその放物線の軸といい,軸と放物線の交点をその放物線の頂点という。
つまり,$y=ax^2$ のグラフは軸が $y$ 軸で,頂点が原点の放物線である。
$a>0$ のとき,$x$ の値が増加すると $x\leq0$ の範囲で $y$ の値は減少し,$x\geq0$ の範囲で $y$ の値は増加する。
$a<0$ のとき,$x$ の値が増加すると $x\leq0$ の範囲で $y$ の値は増加し,$x\geq0$ の範囲で $y$ の値は減少する。
グラフの形状から,$a>0$ のとき,下に凸,$a<0$ のとき,上に凸であるという。
$y=ax^2+q$ のグラフ

ヒロ
次に $y=ax^2+q$ のグラフを考えよう。

ヒロ
$y=ax^2$ との違いは $q$ が足されている部分だね。

ヒロ
つまり,$y=ax^2$ のグラフと比べると,同じ $x$ 座標では $y$ 座標が $q$ だけ大きくなるね。

ヒロ
$q$ が正なら $y$ 軸方向に平行移動させたものになる。
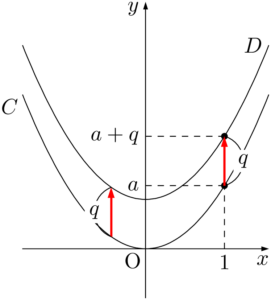
$D:y=ax^2+q$ のグラフ$C:y=ax^2$ のグラフを $y$ 軸方向に $q$ だけ平行移動したもの。
軸は $x=0$,頂点は $(0,~q)$
軸は $x=0$,頂点は $(0,~q)$

$y=a(x-p)^2$ のグラフ

ヒロ
次は $y=a(x-p)^2$ のグラフを考えてみよう。

ヒロ
具体例として,次の問題を考える。
問題$y=(x-1)^2$ のグラフを描け。
【$y=(x-1)^2$ のグラフ】
\begin{align*}
\begin{array}{|c||c|c|c|c|c|c|c|c|}\hline
x & \cdots & -2 & -1 & 0 & 1 & 2 & 3 & \cdots \\\hline
x^2 &\cdots & 4 & 1 & 0 & 1 & 4 & 9 & \cdots \\\hline
(x-1)^2 & \cdots & 9 & 4 & 1 & 0 & 1 & 4 & \cdots \\\hline
\end{array}
\end{align*}
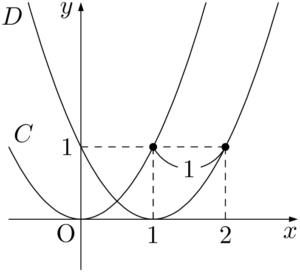
表から,$C:y=x^2$ のグラフと $D:y=(x-1)^2$ のグラフは次のようになり,$D$ は $C$ を $x$ 軸方向に1だけ平行移動したものであることが分かる。\begin{array}{|c||c|c|c|c|c|c|c|c|}\hline
x & \cdots & -2 & -1 & 0 & 1 & 2 & 3 & \cdots \\\hline
x^2 &\cdots & 4 & 1 & 0 & 1 & 4 & 9 & \cdots \\\hline
(x-1)^2 & \cdots & 9 & 4 & 1 & 0 & 1 & 4 & \cdots \\\hline
\end{array}
\end{align*}

$D:y=a(x-p)^2$ のグラフ$C:y=ax^2$ のグラフを $x$ 軸方向に $p$ だけ平行移動したもの。
軸は $x=p$,頂点は $(p,~0)$
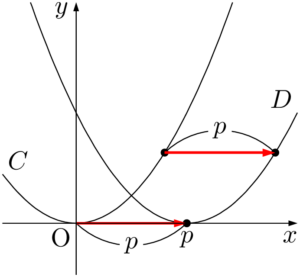
軸は $x=p$,頂点は $(p,~0)$

$y=a(x-p)^2+q$ のグラフ

ヒロ
これは上2つを合わせた考え方になるね。
$D:y=a(x-p)^2+q$ のグラフ$C:y=ax^2$ のグラフを $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動したもの。
軸は $x=p$,頂点は $(p,~q)$
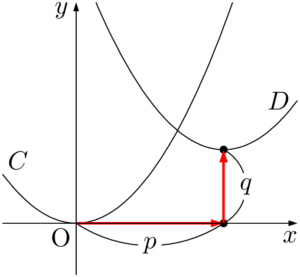
軸は $x=p$,頂点は $(p,~q)$

2次関数の軸と頂点を求める問題

ヒロ
それでは簡単な問題を解くことで,2次関数について復習しておこう。
問題次の2次関数の軸と頂点を求めてグラフを描け。
(1) $y=2(x-1)^2+3$
(2) $y=-(x-2)^2-4$
(3) $y=3\left(x+\dfrac12\right)^2-\dfrac34$
(4) $y=-\dfrac13(x-3)^2+5$
(1) $y=2(x-1)^2+3$
(2) $y=-(x-2)^2-4$
(3) $y=3\left(x+\dfrac12\right)^2-\dfrac34$
(4) $y=-\dfrac13(x-3)^2+5$

ヒロ
2次関数のグラフを描くときは,頂点・$y$ 切片と上に凸や下に凸に注意しよう。
【解答】
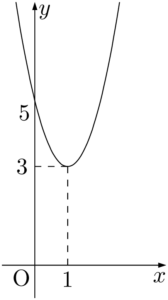
(1) 軸:$x=1$,頂点:$(1,~3)$
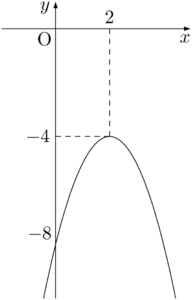
(2) 軸:$x=2$,頂点:$(2,~-4)$
(3) 軸:$x=-\dfrac{1}{2}$,頂点:$\left(-\dfrac{1}{2},~-\dfrac{3}{4}\right)$
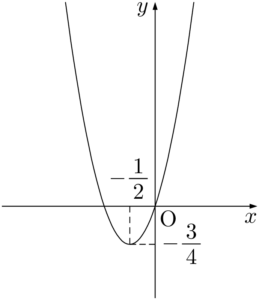
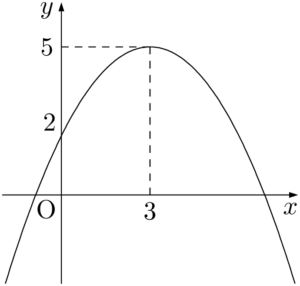
(4) 軸:$x=3$,頂点:$(3,~5)$
(1) 軸:$x=1$,頂点:$(1,~3)$

(2) 軸:$x=2$,頂点:$(2,~-4)$

(3) 軸:$x=-\dfrac{1}{2}$,頂点:$\left(-\dfrac{1}{2},~-\dfrac{3}{4}\right)$

(4) 軸:$x=3$,頂点:$(3,~5)$



















