Contents
多項式の割り算を利用する問題2
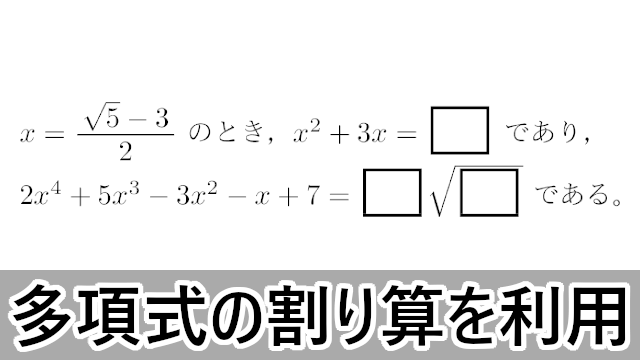
2014年 早稲田大$\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$ の小数部分を $a$ とするとき,$a$ は2次方程式 $x^2+\myBox{ア}\,x+\myBox{イ}=0$ の解であり,$a^3+6a^2-21a+23$ の値は $\myBox{ウ}+\myBox{エ}\sqrt{\myBox{オ}}$ である。
【考え方と解答】
まずは小数部分の $a$ を正確に求めよう。
よって,$\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$ の整数部分は9であり,
次に $a^3+6a^2-21a+23$ の値を求めよう。$(x^3+6x^2-21x+23)\div(x^2+8x-8)$ を計算すると,次のようになる。
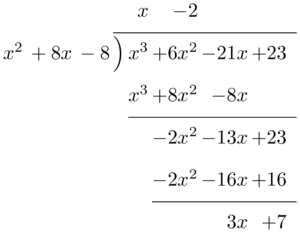
したがって
まずは小数部分の $a$ を正確に求めよう。
\begin{align*}
\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}&=(\sqrt{3}+\sqrt{2})^2 \\[4pt]
&=5+2\sqrt{6}=5+\sqrt{24}
\end{align*}
ここで $4<\sqrt{24}<5$ であるから,$9<5+\sqrt{24}<10$ となる。\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}&=(\sqrt{3}+\sqrt{2})^2 \\[4pt]
&=5+2\sqrt{6}=5+\sqrt{24}
\end{align*}
よって,$\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$ の整数部分は9であり,
\begin{align*} a=\dfrac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}-9=2\sqrt{6}-4 \end{align*}
この結果から $a+4=2\sqrt{6}$ となり,両辺を2乗すると \begin{align*} &(a+4)^2=24 \\[4pt] &a^2+8a-8=0 \end{align*}
したがって,$a$ は2次方程式 $x^2+8x+(-8)=0$ の解である。次に $a^3+6a^2-21a+23$ の値を求めよう。$(x^3+6x^2-21x+23)\div(x^2+8x-8)$ を計算すると,次のようになる。

したがって
\begin{align*} a^3+6a^2-21a+23&=(a^2+8a-8)(a-2)+3a+7 \\[4pt] &=3a-7=3(2\sqrt{6}-4)+7 \\[4pt] &=-5+6\sqrt{6} \end{align*}