1次不等式を満たす整数の個数を求める問題は,定期テストだけでなく,模試などにもよく出る問題です。
苦手な人はできるだけ早い段階で,しっかりと理解して解けるようにしておくことが重要です。
解を表す不等式の等号に注意して,不等式を満たす整数の個数を数えられるようになりましょう。
Contents
定期テストに出題された問題1

ヒロ
それでは次の問題を考えてみよう。
問題1$x$ についての不等式 $3x-6\leqq4x-2<x+a$ を満たす整数が5個あるように定数 $a$ の値の範囲を求めよ。

ヒロ
まずは2つの不等式に分けて,別々に解こう。
$a\leqq b\leqq c$ は2つの不等式$a\leqq b\leqq c$ は
\begin{align*} a\leqq b~~かつ~~b\leqq c \end{align*}
であることを知っておこう。【問題1の考え方と解答】
$3x-6\leqq4x-2<x+a$ より
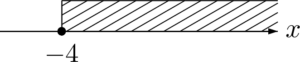
②が表す $x$ の値の範囲は次のようになる。
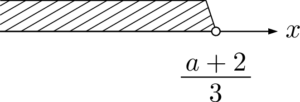
ここで①と②を同時に満たす整数が少なくとも1個存在するためには,$\dfrac{a+2}{3}$ が $-4$ より大きくないといけないことが分かる。このとき①かつ②が表す $x$ の値の範囲は次のようになる。
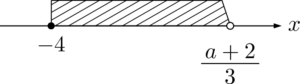
この斜線部分の範囲にある整数が5個となるような $\dfrac{a+2}{3}$ の範囲を考える。
すでに $-4$ の1個は確定しているから,$-4$ より大きい整数を1つずつみていくと,$-4,~-3,~-2,~-1,~0$ で5個の整数になる。0は入るが,1は入らない。つまり,$\dfrac{a+2}{3}$ は0と1の間にあるときは条件を満たすことが分かる。
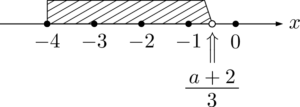
あとは $\dfrac{a+2}{3}$ が0や1に等しいときに斜線部分にある整数の個数が5個になるなら,そのときも答えとなる $a$ の値の範囲に加えないといけない。
ということで,1つずつ調べる。
【$\dfrac{a+2}{3}=0$ のとき】
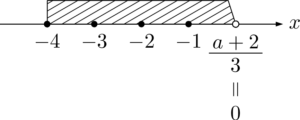
このときは0が斜線部分にないため,斜線部分にある整数は $-4,~-3,~-2,~-1$ の4個となって条件を満たさない。
【$\dfrac{a+2}{3}=1$ のとき】
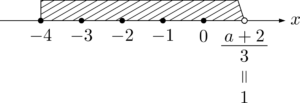
このときは斜線部分にある整数は $-4,~-3,~-2,~-1,~0$ の5個となって条件を満たす。
以上より,条件を満たすのは
$3x-6\leqq4x-2<x+a$ より
\begin{align*} \begin{cases} 3x-6\leqq 4x-2 &\cdots\cdots① \\[4pt] 4x-2<x+a &\cdots\cdots② \end{cases} \end{align*}
①より\begin{align*} &-x\leqq4 \\[4pt] &x\geqq-4 \end{align*}
②より\begin{align*} &3x<a+2 \\[4pt] &x<\dfrac{a+2}{3} \end{align*}
①が表す $x$ の値の範囲は次のようになる。
②が表す $x$ の値の範囲は次のようになる。

ここで①と②を同時に満たす整数が少なくとも1個存在するためには,$\dfrac{a+2}{3}$ が $-4$ より大きくないといけないことが分かる。このとき①かつ②が表す $x$ の値の範囲は次のようになる。

この斜線部分の範囲にある整数が5個となるような $\dfrac{a+2}{3}$ の範囲を考える。
すでに $-4$ の1個は確定しているから,$-4$ より大きい整数を1つずつみていくと,$-4,~-3,~-2,~-1,~0$ で5個の整数になる。0は入るが,1は入らない。つまり,$\dfrac{a+2}{3}$ は0と1の間にあるときは条件を満たすことが分かる。

あとは $\dfrac{a+2}{3}$ が0や1に等しいときに斜線部分にある整数の個数が5個になるなら,そのときも答えとなる $a$ の値の範囲に加えないといけない。
ということで,1つずつ調べる。
【$\dfrac{a+2}{3}=0$ のとき】

このときは0が斜線部分にないため,斜線部分にある整数は $-4,~-3,~-2,~-1$ の4個となって条件を満たさない。
【$\dfrac{a+2}{3}=1$ のとき】

このときは斜線部分にある整数は $-4,~-3,~-2,~-1,~0$ の5個となって条件を満たす。
以上より,条件を満たすのは
\begin{align*}
0<\dfrac{a+2}{3}\leqq1
\end{align*}
のときで,これを解くと0<\dfrac{a+2}{3}\leqq1
\end{align*}
\begin{align*} &0<a+2\leqq3 \\[4pt] &-2<a\leqq1 \end{align*}
定期テストに出題された問題2

ヒロ
それでは次の問題を考えてみよう。
問題2$x$ についての不等式
\begin{align*}
\begin{cases}
3x-6<8-4x \\[4pt]
4x+a\geqq x+4
\end{cases}
\end{align*}
がある。ただし $a$ は正の定数とする。この不等式を同時に満たす $x$ のうちで整数は7つだけであるという。このとき定数 $a$ の値の範囲を求めよ。\begin{cases}
3x-6<8-4x \\[4pt]
4x+a\geqq x+4
\end{cases}
\end{align*}

ヒロ
問題1と同じように解こう。
【問題2の考え方と解答】
$3x-6<8-4x$ より

ここで $\dfrac{-a+4}{3}$ が $-6$ や $-5$ と等しくなるときの斜線部分に含まれる整数の個数を調べる。
【$\dfrac{-a+4}{3}=-6$ のとき】
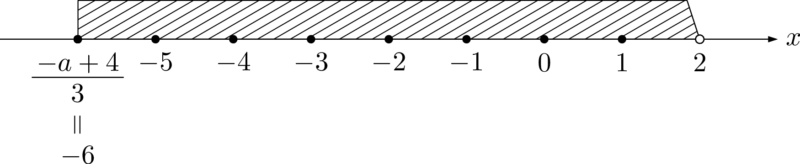
このとき斜線部分に含まれる整数は8個となり条件を満たさない。
【$\dfrac{-a+4}{3}=-5$ のとき】
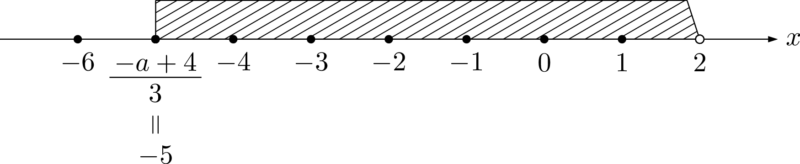
このとき斜線部分に含まれる整数は7個となり条件を満たす。
したがって
$3x-6<8-4x$ より
\begin{align*}
&7x<14 \\[4pt]
&x<2
\end{align*}
$4x+a\geqq x+4$ より&7x<14 \\[4pt]
&x<2
\end{align*}
\begin{align*}
&3x\geqq-a+4 \\[4pt]
&x\geqq\dfrac{-a+4}{3}
\end{align*}
$a<0$ のとき $\dfrac{-a+4}{3}<2$ が成り立つから,①と②を同時に満たす $x$ は&3x\geqq-a+4 \\[4pt]
&x\geqq\dfrac{-a+4}{3}
\end{align*}
\begin{align*}
\dfrac{-a+4}{3}\leqq x<2
\end{align*}
となる。この不等式を満たす整数がちょうど7つになるのは次のようになるときである。\dfrac{-a+4}{3}\leqq x<2
\end{align*}

ここで $\dfrac{-a+4}{3}$ が $-6$ や $-5$ と等しくなるときの斜線部分に含まれる整数の個数を調べる。
【$\dfrac{-a+4}{3}=-6$ のとき】

このとき斜線部分に含まれる整数は8個となり条件を満たさない。
【$\dfrac{-a+4}{3}=-5$ のとき】

このとき斜線部分に含まれる整数は7個となり条件を満たす。
したがって
\begin{align*}
&-6<\dfrac{-a+4}{3}\leqq-5 \\[4pt]
&-18<-a+4\leqq-15 \\[4pt]
&-22<-a\leqq-19 \\[4pt]
&19\leqq a<22
\end{align*}
&-6<\dfrac{-a+4}{3}\leqq-5 \\[4pt]
&-18<-a+4\leqq-15 \\[4pt]
&-22<-a\leqq-19 \\[4pt]
&19\leqq a<22
\end{align*}

ヒロ
このような問題において,$\dfrac{-a+4}{3}$ が2つの整数 $-6$ と $-5$ の間にあることを理解できる人は多いだろう。

ヒロ
等号の部分が良く分からない人は「もし $\dfrac{-a+4}{3}$ が $-6$ と等しかったらどうなるんだろう?」と落ち着いて考えることが重要である。

ヒロ
しっかり考えることで理解することができ,このタイプの問題を得点源とすることができる。


















