多項式の除法の方法には,筆算・組立除法・暗算の3つの方法があります。筆算・組立除法でも面倒だなぁと感じる人は暗算で割り算を出来るようにしましょう。
筆算や組立除法より速くなる可能性があります。ここでは多項式の除法を暗算でする方法について説明します。
暗算による除法

まずは基礎の確認をしておこう。商と余りはそれぞれ何次式か分かる?

3次式を2次式で割っているから,商は1次式で,余りは1次式か定数ですね。

そうだね。あとは割られる式と割る式,商,余りの関係を確認しておこうか。

ということで・・・
x^3-5x^2+3x+4=(x^2-2x+3)(\diamondsuit x+\heartsuit)+\spadesuit x+\clubsuit
\end{align*}

こんな風に表すことができるはずだよね?

そうですね。

まずは $\diamondsuit$ から考えよう。

右辺を展開すると,当然左辺になるよね。右辺の括弧の中の最高次どうしの積が左辺の最高次になるから,$\diamondsuit=1$ と分かるはず。
x^3-5x^2+3x+4=(x^2-2x+3)(x+\heartsuit)+\spadesuit x+\clubsuit
\end{align*}

次に $\heartsuit$ を求めよう。そのために,$x^2$ の項に着目しよう。
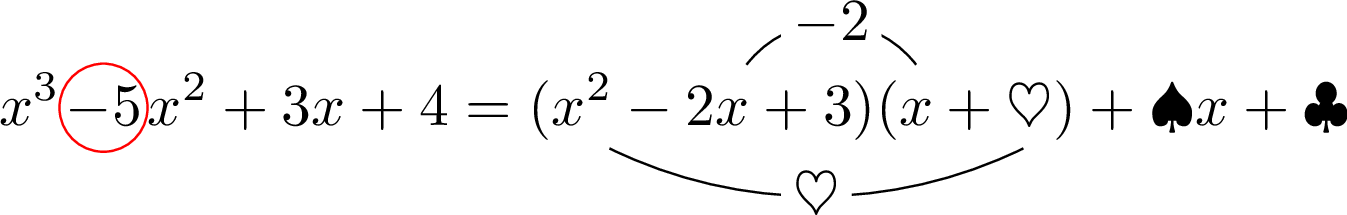

$-2+\heartsuit=-5$ となるように $\heartsuit$ を決めればいいよね?

$\heartsuit=-3$ ですね!

そうだね。この時点でこうなる。
x^3-5x^2+3x+4=(x^2-2x+3)(x-3)+\spadesuit x+\clubsuit
\end{align*}

あとは余りだね。$x$ の項に着目しよう。
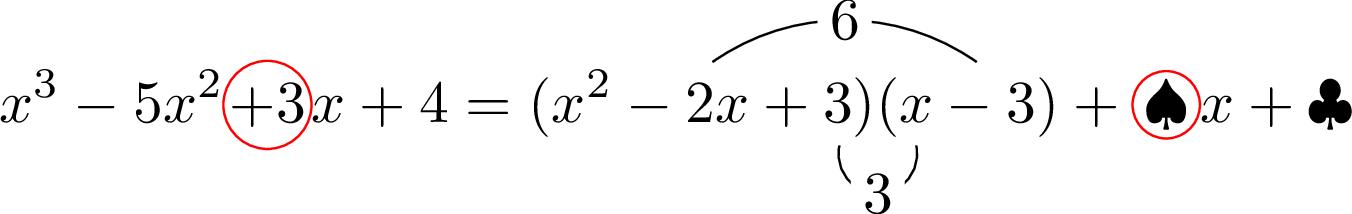

$3=6+3+\spadesuit$ となるように $\spadesuit$ を決めると,$\spadesuit=-6$ となるね。
x^3-5x^2+3x+4=(x^2-2x+3)(x-3)-6x+\clubsuit
\end{align*}

最後は余りの定数項 $\clubsuit$ だね。これは定数項に着目しよう。
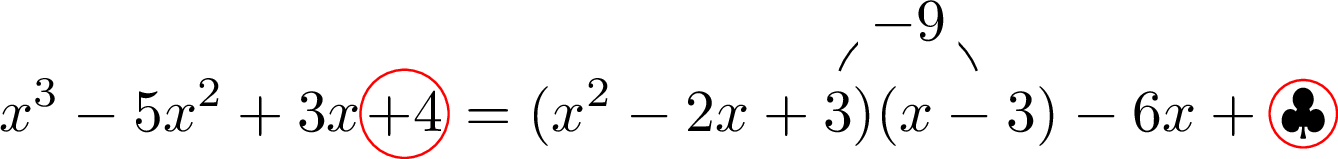

$4=-9+\clubsuit$ となるように $\clubsuit$ を決めると,$\clubsuit=13$ となるね。
x^3-5x^2+3x+4=(x^2-2x+3)(x-3)-6x+13
\end{align*}

ということで,商は $x-3$,余りは $-6x+13$ ですね。

慣れれば組立除法を使うより速く計算できるようになるよ。

頑張ります!
練習

じゃあ軽く練習しておこう。

まず問題文の条件を等式で表すとこうなります。
x^4-2x^3+x-2=P(x)(x^2+1)+3x-1
\end{align*}

これを変形して・・・
P(x)(x^2+1)=x^4-2x^3-2x-1
\end{align*}

こうなるから,$x^4-2x^3-2x-1$ を $x^2+1$ で割れば $P(x)$ が求まります。
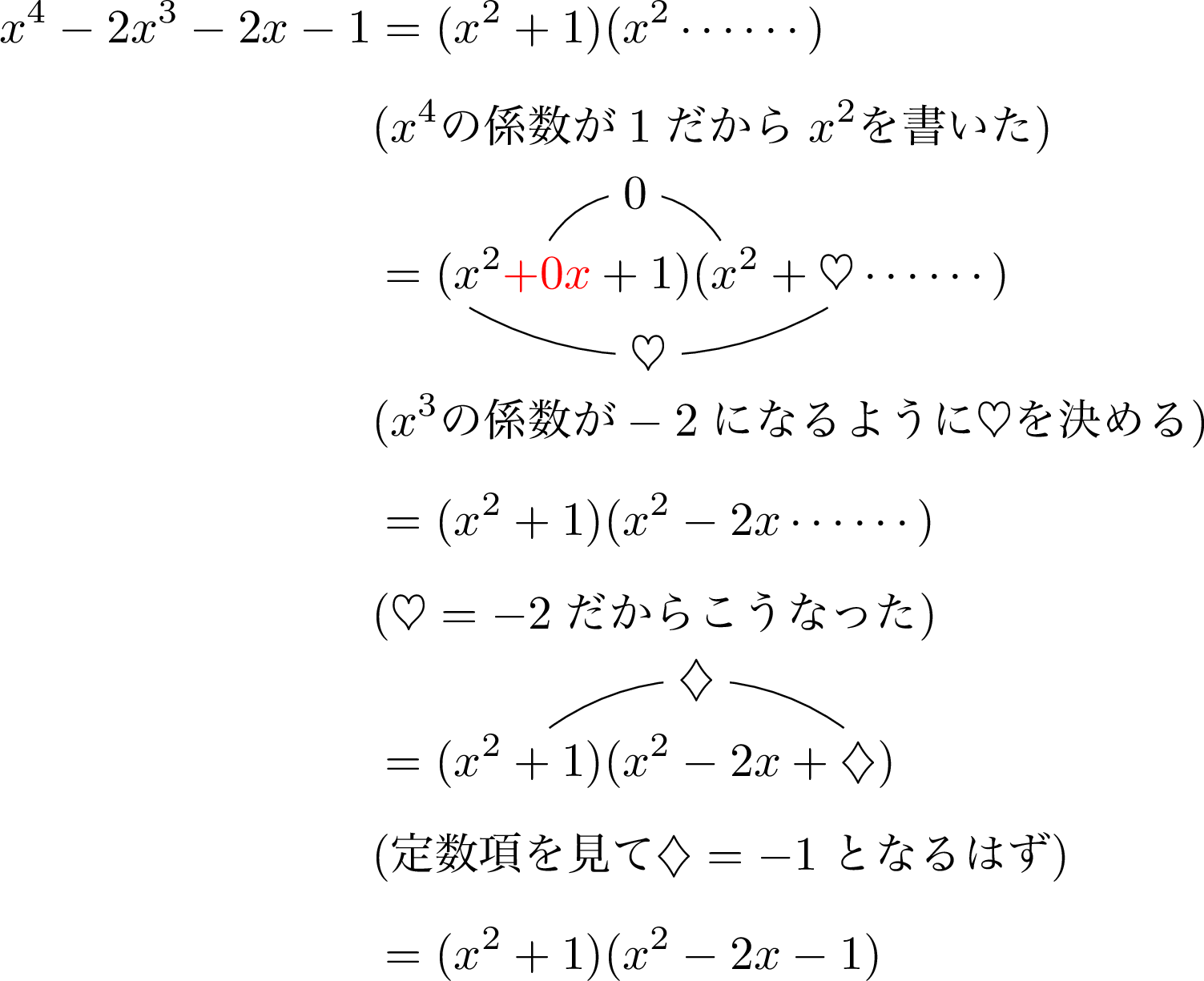

最後に計算が合ってるか確認しておきます。
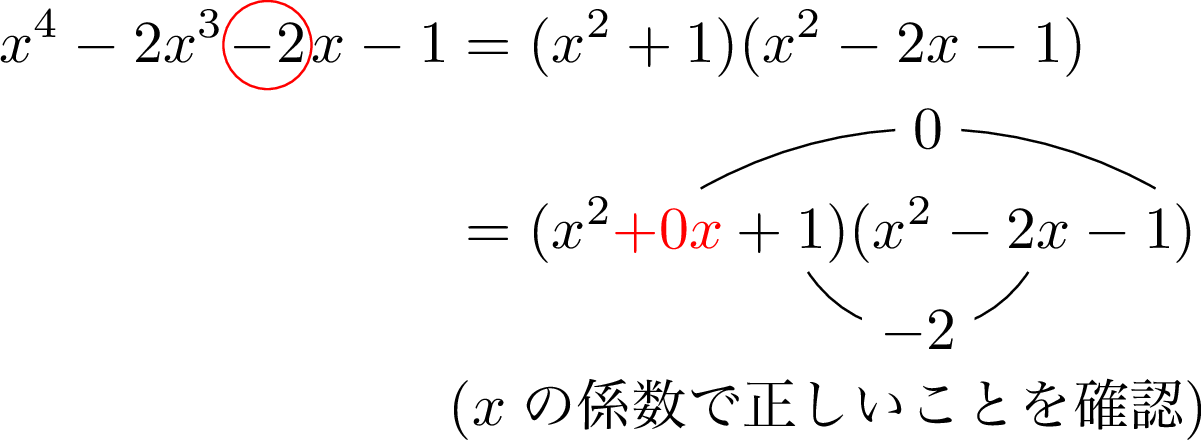

ということで,$P(x)=x^2-2x-1$ ですね。

オッケーだね。
まとめ

多項式の除法には,3つの方法があるけど,より速い方法でできるようにしよう。
- 筆算
- 組立除法
- 暗算

ただし,何より重要なのは正確さ。いくら速くても間違いが多いのでは意味がないから注意しよう!



















