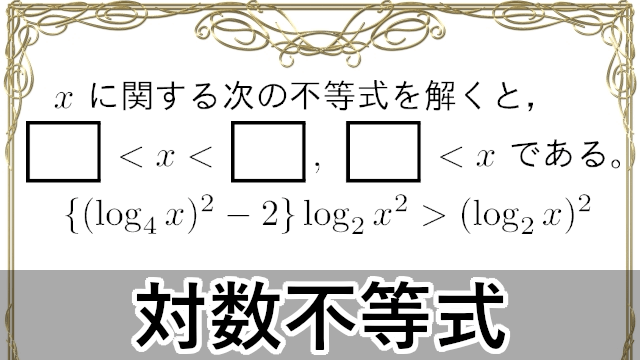
ここでは,対数不等式について説明します。
対数不等式の問題では,底と1との大小関係に注意しましょう。
また,底が異なる項がある場合は,底を揃える必要があるため,底の変換公式を使いこなせるようにしておきましょう。
Contents
2019年 大阪工業大
2019年 大阪工業大不等式
\begin{align*}
\log_2(2n^2+1)>\log_2(11n-8)
\end{align*}
を満たすような最小の自然数 $n$ は,$n=\myhako$ である。\log_2(2n^2+1)>\log_2(11n-8)
\end{align*}
【考え方と解答】
$n$ は自然数であるから,真数 $2n^2+1$,$11n-8$ は常に正である。
底が2で1より大きいから
これを満たす最小の自然数 $n$ は,$n=5$
$n$ は自然数であるから,真数 $2n^2+1$,$11n-8$ は常に正である。
底が2で1より大きいから
\begin{align*}
&2n^2+1>11n-8 \\[4pt]
&2n^2-11n+9>0 \\[4pt]
&(n-1)(2n-9)>0
\end{align*}
$n-1\geqq0$ であるから,$2n-9>0$&2n^2+1>11n-8 \\[4pt]
&2n^2-11n+9>0 \\[4pt]
&(n-1)(2n-9)>0
\end{align*}
これを満たす最小の自然数 $n$ は,$n=5$