Contents
2020年 大阪薬科大
2020年 大阪薬科大不等式
\begin{align*}
\log_{\frac{1}{3}}n+\log_{\frac{1}{3}}(n+2)-\log_{\frac{1}{3}}(2n-1)-\log_{\frac{1}{3}}3>0
\end{align*}
を満たす自然数 $n$ は $\myhako$ である。\log_{\frac{1}{3}}n+\log_{\frac{1}{3}}(n+2)-\log_{\frac{1}{3}}(2n-1)-\log_{\frac{1}{3}}3>0
\end{align*}
【考え方と解答】
対数の差を1つの対数で表すと,分母が文字を含む式になり,0になることがないかなど,色々と気にする部分が生じてしまう。そのため,対数の差が現れないように式変形するのが,結果的に楽になるだろう。
与えられた不等式より
対数の差を1つの対数で表すと,分母が文字を含む式になり,0になることがないかなど,色々と気にする部分が生じてしまう。そのため,対数の差が現れないように式変形するのが,結果的に楽になるだろう。
与えられた不等式より
\begin{align*}
&\log_{\frac{1}{3}}n+\log_{\frac{1}{3}}(n+2)>\log_{\frac{1}{3}}(2n-1)+\log_{\frac{1}{3}}3 \\[4pt]
&\log_{\frac{1}{3}}n(n+2)>\log_{\frac{1}{3}}3(2n-1)
\end{align*}
底が $0<\dfrac{1}{3}<1$ であるから &\log_{\frac{1}{3}}n+\log_{\frac{1}{3}}(n+2)>\log_{\frac{1}{3}}(2n-1)+\log_{\frac{1}{3}}3 \\[4pt]
&\log_{\frac{1}{3}}n(n+2)>\log_{\frac{1}{3}}3(2n-1)
\end{align*}
\begin{align*} &n(n+2)<3(2n-1) \\[4pt] &n^2-4n+3<0 \\[4pt] &(n-1)(n-3)<0 \\[4pt] &1<n<3 \end{align*}
よって,与えられた不等式を満たす自然数 $n$ は $n=2$ である。2019年 獨協医科大
2019年 獨協医科大$a$ は $a>0,~a\neq1$ を満たす定数とする。$x$ の不等式
\begin{align*}
\log_a(x-3)-\log_{a^2}(5-x)<\log_{a}\sqrt{x} \end{align*}
の解は \log_a(x-3)-\log_{a^2}(5-x)<\log_{a}\sqrt{x} \end{align*}
\begin{align*} &a>1~のとき~\myhako<x<\dfrac{\myhako}{\myhako} \\[4pt] &0<a<1~のとき~\dfrac{\myhako}{\myhako}<x<\myhako \end{align*}
である。【考え方と解答】
まず,真数条件から定義域を求めよう。真数は正であるから
まず,真数条件から定義域を求めよう。真数は正であるから
\begin{align*} x-3>0~かつ~5-x>0~かつ~\sqrt{x}>0
\end{align*}
よって,$3<x<5~\cdots\cdots①$ 底を $a$ に揃える人が多いだろう。しかし,楽をするために底を $a^2$ に揃えることにする。対数に関連する記事を最初から読んでいる人にとっては,この考え方は当たり前に感じるかもしれない。念のために書いておくと,公式「$\log_ab=\log_{a^n}b^n$」を利用する。与えられた不等式より \end{align*}
\begin{align*} &\log_{a^2}(x-3)^2<\log_{a^2}x+\log_{a^2}(5-x) \\[4pt] &\log_{a^2}(x-3)^2<\log_{a^2}x(5-x) \end{align*}
$a>1$ のとき\begin{align*}
&(x-3)^2<x(5-x) \\[4pt] &2x^2-11x+9<0 \\[4pt] &(x-1)(2x-9)<0 \\[4pt] &1<x<\dfrac{9}{2} \end{align*}
①より,$3<x<\dfrac{9}{2}$ $0<a<1$ のとき &(x-3)^2<x(5-x) \\[4pt] &2x^2-11x+9<0 \\[4pt] &(x-1)(2x-9)<0 \\[4pt] &1<x<\dfrac{9}{2} \end{align*}
\begin{align*} &(x-3)^2>x(5-x) \\[4pt]
&(x-1)(2x-9)>0 \\[4pt]
&x<1,~\dfrac{9}{2}<x \end{align*}
①より,$\dfrac{9}{2}<x<5$&(x-1)(2x-9)>0 \\[4pt]
&x<1,~\dfrac{9}{2}<x \end{align*}
2020年 明治大
2020年 明治大$x$ に関する次の不等式を解くと,$\myhako<x<\myhako,~\myhako<x$ である。
\begin{align*} \{(\log_4x)^2-2\}\log_2x^2>(\log_2x)^2
\end{align*}
\end{align*}
【考え方と解答】
真数は正であるから,$x>0$
与えられた不等式より
真数は正であるから,$x>0$
与えられた不等式より
\begin{align*}
&\left\{\left(\dfrac{1}{2}\log_2x\right)^2-2\right\}\Cdota2\log_2x>(\log_2x)^2 \\[4pt]
&\dfrac{1}{2}(\log_2x)^3-4\log_2x>(\log_2x)^2 \\[4pt]
&(\log_2x)^3-2(\log_2x)^2-8\log_2x>0 \\[4pt]
&\log_2x\{(\log_2x)^2-2\log_2x-8\}>0 \\[4pt]
&\log_2x(\log_2x-4)(\log_2x+2)>0 \\[4pt]
&-2<\log_2x<0,~4<\log_2x \\[4pt] &\dfrac{1}{4}<x<1,~16<x \end{align*}
&\left\{\left(\dfrac{1}{2}\log_2x\right)^2-2\right\}\Cdota2\log_2x>(\log_2x)^2 \\[4pt]
&\dfrac{1}{2}(\log_2x)^3-4\log_2x>(\log_2x)^2 \\[4pt]
&(\log_2x)^3-2(\log_2x)^2-8\log_2x>0 \\[4pt]
&\log_2x\{(\log_2x)^2-2\log_2x-8\}>0 \\[4pt]
&\log_2x(\log_2x-4)(\log_2x+2)>0 \\[4pt]
&-2<\log_2x<0,~4<\log_2x \\[4pt] &\dfrac{1}{4}<x<1,~16<x \end{align*}

ヒロ
最後の部分について補足しておく。
【正になる範囲】
$\log_2x=t$ とすると,$x$ が正の実数を動くとき,$t$ はすべての実数値をとり得る。
簡単なのは3次関数のグラフを利用する方法である。$y=f(t)$ のグラフを描くと次のようになる。
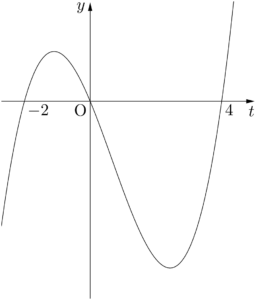
グラフから,$f(t)>0$ となる $t$ の値の範囲は
このように3つの多項式の積の形になっていれば,3次関数のグラフを描くのは簡単で,素早く不等式を解くこともできる。ただし,因数の数が増えたり分数関数になったりするとグラフを描くこと自体が難しくなる場合がある。そんなときのために,別の方法も説明しておく。
絶対値を含む方程式や不等式のときのように,3つの因数の符号に着目する。
$\log_2x=t$ とすると,$x$ が正の実数を動くとき,$t$ はすべての実数値をとり得る。
\begin{align*} f(t)=t(t-4)(t+2) \end{align*}
として $f(t)>0$ となる $t$ の値の範囲を考える。簡単なのは3次関数のグラフを利用する方法である。$y=f(t)$ のグラフを描くと次のようになる。

グラフから,$f(t)>0$ となる $t$ の値の範囲は
\begin{align*}
-2<t<0,~4<t \end{align*}
となることが分かる。-2<t<0,~4<t \end{align*}
このように3つの多項式の積の形になっていれば,3次関数のグラフを描くのは簡単で,素早く不等式を解くこともできる。ただし,因数の数が増えたり分数関数になったりするとグラフを描くこと自体が難しくなる場合がある。そんなときのために,別の方法も説明しておく。
絶対値を含む方程式や不等式のときのように,3つの因数の符号に着目する。
\begin{align*} \def\arraystretch{1.3} \begin{array}{|c||c|c|c|c|c|c|c|}\hline t & \cdots & -2 & \cdots & 0 & \cdots & 4 & \cdots \\\hline\hline t-4 & – & – & – & 0 & + & + & + \\\hline t & – & – & – & & – & 0 & + \\\hline t+2 & – & 0 & + & + & + & + & + \\\hline\hline f(t) & – & 0 & + & 0 & – & 0 & + \\\hline \end{array} \end{align*}
$t$ の値に応じて変化する3つの因数の符号を確認することで,$f(t)$ の符号も分かる。