Contents
2020年 北里大
2020年 北里大$\dfrac{1}{2}\leqq x\leqq128$ のとき,$\log_2x$ のとり得る値の範囲は $\myhako$ であり,
\begin{align*}
f(x)=-(\log_2x^2)^2+12\log_2\dfrac{x}{2}
\end{align*}
の最大値は $\myhako$ である。f(x)=-(\log_2x^2)^2+12\log_2\dfrac{x}{2}
\end{align*}
【考え方と解答】
底が1より大きいから
底が1より大きいから
\begin{align*}
&\log_2\dfrac{1}{2}\leqq\log_2x\leqq\log_2128 \\[4pt]
&-1\leqq\log_2x\leqq7
\end{align*}
$\log_2x=t$ とおくと,$-1\leqq t\leqq7$ であり,&\log_2\dfrac{1}{2}\leqq\log_2x\leqq\log_2128 \\[4pt]
&-1\leqq\log_2x\leqq7
\end{align*}
\begin{align*}
f(x)&=-(2\log_2x)^2+12(\log_2x-1) \\[4pt]
&=-4t^2+12t-12 \\[4pt]
&=-4\left(t-\dfrac{3}{2}\right)^2-3
\end{align*}
右辺を $g(t)$ とおくと,$y=g(t)$ のグラフは上に凸の放物線で,軸 $t=\dfrac{3}{2}$ が定義域 $-1\leqq t\leqq7$ 内にあるから,$t=\dfrac{3}{2}$ で $g(t)$ すなわち $f(x)$ は最大値 $-3$ をとる。f(x)&=-(2\log_2x)^2+12(\log_2x-1) \\[4pt]
&=-4t^2+12t-12 \\[4pt]
&=-4\left(t-\dfrac{3}{2}\right)^2-3
\end{align*}

ヒロ
ここで1つ余談をしておく。
対数の式変形で当たり前のように行っている変形が,実は当たり前でないときがある。例えば $\log_ax^2$ を変形するとき
\begin{align*}
\log_ax^2=2\log_ax
\end{align*}
としてしまうが,これは正しい変形ではない。真数条件に着目すると,$x^2>0$ より定義域は $x\neq0$ となる。$x>0$ のときは正しい式になるが,$x<0$ のときは $2\log_ax$ の真数が負となるため値が定義されなくなってしまう。したがって,正しく変形するには \log_ax^2=2\log_ax
\end{align*}
\begin{align*} \log_ax^2=2\log_a\abs{x} \end{align*}
としなければならない。この話をしたところで「そんな変形したことがない」と言われそうだが,それはほとんどの問題では $\log_ax^2$ が現れる式では $\log_ax$ も含んでいるからである。$\log_ax^2$ と $\log_ax$ が混在している式では,真数が正になるのは $x>0$ のときであり,特に考えなくても $\log_ax^2=2\log_ax$ が成り立ってしまう。
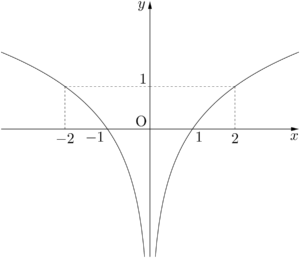
このことに注意していないと「$y=\log_2x^2$ のグラフを描け。」という問題で,$y=2\log_2x$ と変形するとと $x>0$ の部分しか定義されていない間違ったグラフを描いてしまう。正しく変形すると $y=2\log_2\abs{x}$ となり,グラフは次のようになる。
2019年 立教大
2019年 立教大正の数 $x,~y$ が $xy=16$ を満たすとき,$(\log_2x)^3+(\log_2y)^3$ の最小値は $\myhako$ である。
【考え方と解答】
2変数関数の最小値を求める問題では,1変数関数に変形できるかどうかを考えよう。この問題では $xy=16$ を利用する。底を2とする対数をとると
2変数関数の最小値を求める問題では,1変数関数に変形できるかどうかを考えよう。この問題では $xy=16$ を利用する。底を2とする対数をとると
\begin{align*}
&\log_2xy=\log_216 \\[4pt]&\log_2x+\log_2y=4 \\[4pt]&\log_2y=4-\log_2x
\end{align*}
$\log_2x=X$ とおくと $x$ が正の数であるから $X$ はすべての実数をとり得る。&\log_2xy=\log_216 \\[4pt]&\log_2x+\log_2y=4 \\[4pt]&\log_2y=4-\log_2x
\end{align*}
\begin{align*}
&(\log_2x)^3+(\log_2y)^3 \\[4pt]&=X^3+(4-X)^3 \\[4pt]&=12X^2-48X+64 \\[4pt]&=12(X-2)^2+16
\end{align*}
よって,求める最小値は16である。&(\log_2x)^3+(\log_2y)^3 \\[4pt]&=X^3+(4-X)^3 \\[4pt]&=12X^2-48X+64 \\[4pt]&=12(X-2)^2+16
\end{align*}
2019年 早稲田大
2019年 早稲田大$x$ が $\dfrac{1}{3}\leqq x\leqq9$ の範囲を動くとき,関数
\begin{align*}
f(x)=\left(\log_{\frac{1}{3}}9x\right)\left(\log_{\frac{1}{3}}\dfrac{x}{3}\right)
\end{align*}
を考える。$f(x)$ は $x=\myhako$ のとき最大値 $\myhako$ をとり,$x=\myhako$ のとき最小値 $\myhako$ をとる。f(x)=\left(\log_{\frac{1}{3}}9x\right)\left(\log_{\frac{1}{3}}\dfrac{x}{3}\right)
\end{align*}
【考え方と解答】
$\log_{\frac{1}{3}}x=t$ とおくと,底が $0<\dfrac{1}{3}<1$ であるから,$\dfrac{1}{3}\leqq x\leqq9$ のとき $-2\leqq t\leqq1$ となる。$f(x)$ を $t$ で表すと
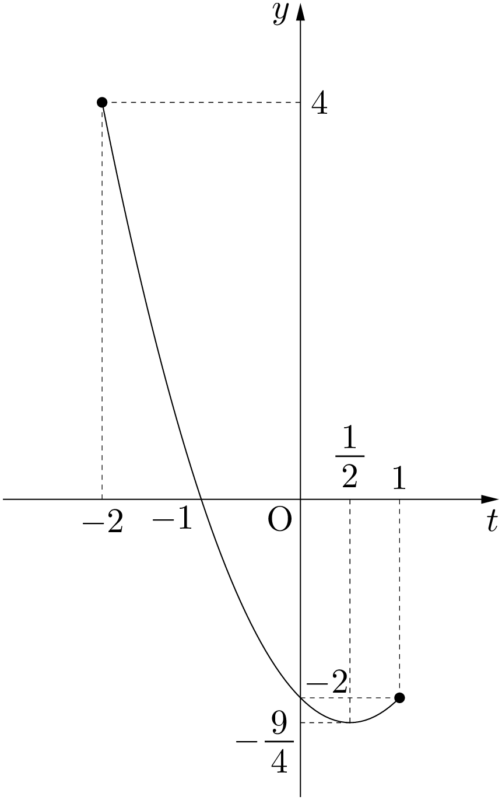
グラフより $t=-2$ のとき最大となり,$t=\dfrac{1}{2}$ のとき最小となる。
$t=-2$ のとき
$\log_{\frac{1}{3}}x=t$ とおくと,底が $0<\dfrac{1}{3}<1$ であるから,$\dfrac{1}{3}\leqq x\leqq9$ のとき $-2\leqq t\leqq1$ となる。$f(x)$ を $t$ で表すと
\begin{align*} f(x)&=\left(\log_{\frac{1}{3}}9+\log_{\frac{1}{3}}x\right)\left(\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}3\right) \\[4pt] &=(t-2)(t+1) \\[4pt] &=\left(t-\dfrac{1}{2}\right)^2-\dfrac{9}{4} \end{align*}

グラフより $t=-2$ のとき最大となり,$t=\dfrac{1}{2}$ のとき最小となる。
$t=-2$ のとき
\begin{align*} &\log_{\frac{1}{3}}x=-2 \\[4pt] &x=\left(\dfrac{1}{3}\right)^{-2}=9 \end{align*}
$t=\dfrac{1}{2}$ のとき \begin{align*} &\log_{\frac{1}{3}}x=\dfrac{1}{2} \\[4pt] &x=\left(\dfrac{1}{3}\right)^{\frac{1}{2}}=\dfrac{1}{\sqrt{3}} \end{align*}
したがって,$x=9$ のとき最大値4をとり,$x=\dfrac{1}{\sqrt{3}}$ のとき最小値 $-\dfrac{9}{4}$ をとる。


















