Contents
指数関数のグラフの特徴

ヒロ
指数関数 $y=a^x~(a>0,~a\neq1)$ のグラフの特徴をまとめておく。
$y=a^x~(a>1)$ のグラフの特徴
- グラフの概形
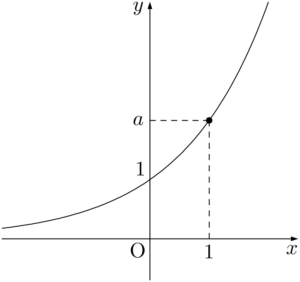
- $x$ の値が増加すると常に $y$ の値も増加する。
- 点 $(0,~1)$ を通る。
- $x$ 軸が漸近線である。

ヒロ
次は $0<a<1$ のときの特徴。
$y=a^x~(0<a<1)$ のグラフの特徴
- グラフの概形
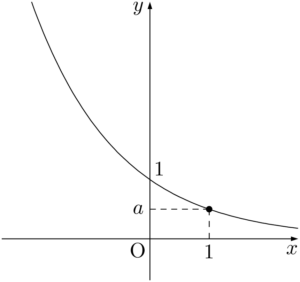
- $x$ の値が増加すると常に $y$ の値が減少する。
- 点 $(0,~1)$ を通る。
- $x$ 軸が漸近線である。

ヒロ
下のアニメーションでは,底 $a$ の値に応じて,$y=a^x$ のグラフがどのように変化するかを確認することができる。
2014年 松山大
2014年 松山大$y=10^{-x}$ のグラフは $\myhako$ である。
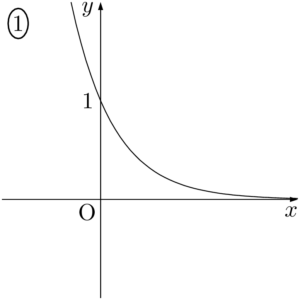
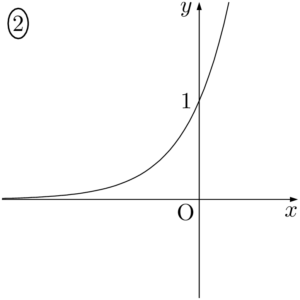
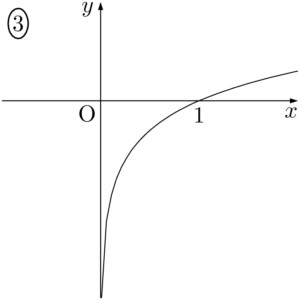
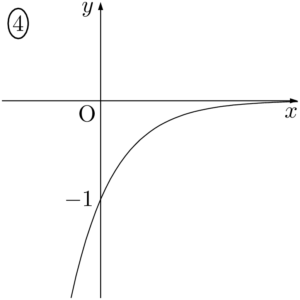
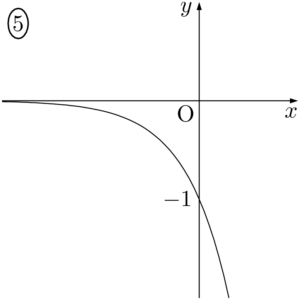





【考え方と解答】
$y=10^{-x}$ は $y=\left(\dfrac{1}{10}\right)^x$ と変形できるから,このグラフは①である。
$y=10^{-x}$ は $y=\left(\dfrac{1}{10}\right)^x$ と変形できるから,このグラフは①である。
2014年 神戸薬科大
2014年 神戸薬科大関数 $y=2^x$ のグラフを $y$ 軸で対称移動させたのち,$x$ 軸方向に $-2$ だけ平行移動させたグラフの方程式は $\myhako$ である。
【考え方と解答】
グラフを平行移動や対称移動させたときに,その方程式がどのように変わるかが分かっていれば簡単だろう。
$y=2^x$ のグラフを $y$ 軸で対称移動させたグラフの方程式は
グラフを平行移動や対称移動させたときに,その方程式がどのように変わるかが分かっていれば簡単だろう。
$y=2^x$ のグラフを $y$ 軸で対称移動させたグラフの方程式は
\begin{align*}
y=2^{-x}
\end{align*}
である。このグラフをさらに $x$ 軸方向に $-2$ だけ平行移動させたグラフの方程式はy=2^{-x}
\end{align*}
\begin{align*}
y=2^{-(x+2)}
\end{align*}
y=2^{-(x+2)}
\end{align*}


















