Contents
命題の証明と領域【京都教育大】
2011年 京都教育大$x,~y$ は実数とする。$x^2+y^2-1<0$ ならば $x^2-2x+y^2<3$ であることを示せ。
【考え方と解答】
与えられている2つの不等式の領域を図示できるため,領域の包含関係を確認する。
$x^2+y^2-1<0$ と $x^2-2x+y^2<3$ が表す領域をそれぞれ $A,~B$ とすると,$A$ は原点を中心とする半径1の円の内部を表し,$B$ は点 $(1,~0)$ を中心とする半径2の円の内部を表す。
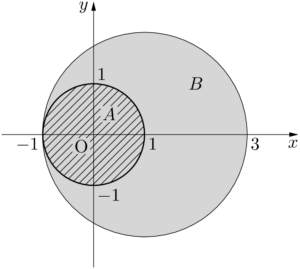
領域 $A$ が領域 $B$ に含まれるから,$x^2+y^2-1<0$ ならば $x^2-2x+y^2<3$ である。
与えられている2つの不等式の領域を図示できるため,領域の包含関係を確認する。
$x^2+y^2-1<0$ と $x^2-2x+y^2<3$ が表す領域をそれぞれ $A,~B$ とすると,$A$ は原点を中心とする半径1の円の内部を表し,$B$ は点 $(1,~0)$ を中心とする半径2の円の内部を表す。

領域 $A$ が領域 $B$ に含まれるから,$x^2+y^2-1<0$ ならば $x^2-2x+y^2<3$ である。
命題が成り立つように定数の範囲を定める【学習院大】
2020年 学習院大命題
「実数 $x,~y$ が $x^2+y^2<1$ をみたすならば,$x^2+x+y^2+a<0$ である」 が真であるような実数 $a$ の範囲を求めよ。
「実数 $x,~y$ が $x^2+y^2<1$ をみたすならば,$x^2+x+y^2+a<0$ である」 が真であるような実数 $a$ の範囲を求めよ。
【考え方と解答】
$x^2+y^2<1$ と $x^2+x+y^2+a<0$ が表す領域をそれぞれ $A,~B$ とする。与えられた命題が真であるのは,領域 $A$ が領域 $B$ に含まれるときである。
ここで,領域 $A$ は原点を中心とする半径1の円の内部を表す。また,$x^2+x+y^2+a<0$ を変形すると
領域 $A$ が領域 $B$ に含まれるのは,下図のようになるときである。
上図のようになるのは,$r\geqq\text{OA}+1$ となるときであるから
$x^2+y^2<1$ と $x^2+x+y^2+a<0$ が表す領域をそれぞれ $A,~B$ とする。与えられた命題が真であるのは,領域 $A$ が領域 $B$ に含まれるときである。
ここで,領域 $A$ は原点を中心とする半径1の円の内部を表す。また,$x^2+x+y^2+a<0$ を変形すると
\begin{align*} \left(x+\dfrac{1}{2}\right)^2+y^2<\dfrac{1}{4}-a \end{align*}
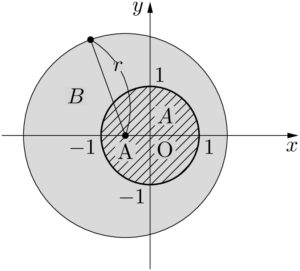
となるから,$a\geqq\dfrac{1}{4}$ のときは領域 $B$ は空集合である。$a<\dfrac{1}{4}$ のときは中心A$\left(-\dfrac{1}{2},~0\right)$,半径 $r=\sqrt{\dfrac{1}{4}-a}$ の円の内部を表す。領域 $A$ が領域 $B$ に含まれるのは,下図のようになるときである。

上図のようになるのは,$r\geqq\text{OA}+1$ となるときであるから
\begin{align*} &\sqrt{\dfrac{1}{4}-a}\geqq\dfrac{1}{2}+1=\dfrac{3}{2} \end{align*}
両辺を2乗すると \begin{align*} &\dfrac{1}{4}-a\geqq\dfrac{9}{4} \\[4pt] &a\leqq-2 \end{align*}




















