Contents
必要十分条件と領域【立教大】
2020年 立教大$a$ を正の実数とし,$x,~y$ を実数とする。$x,~y$ に関する条件 $A,~B$ を次で定める。
1. 必要条件であるが,十分条件でない
2. 十分条件であるが,必要条件でない
3. 必要十分条件である
4. 必要条件でも十分条件でもない
\begin{align*}
&A:\abs{x}+\abs{y}\leqq a \\[4pt]&B:\abs{x}\leqq1~~かつ~\abs{y}\leqq1
\end{align*}
$a=1$ のとき,$A$ は $B$ であるための $\myhako$。$a=2$ のとき,$A$ は $B$ であるための $\myhako$。このとき,以下の選択肢1~4の中から最も適切な番号を解答用紙の所定欄に記入せよ。&A:\abs{x}+\abs{y}\leqq a \\[4pt]&B:\abs{x}\leqq1~~かつ~\abs{y}\leqq1
\end{align*}
1. 必要条件であるが,十分条件でない
2. 十分条件であるが,必要条件でない
3. 必要十分条件である
4. 必要条件でも十分条件でもない
【考え方と解答】
$a$ の値にかかわらず,$B$ が表す領域は変わらないから,$B$ が表す領域を図示することから始める。
$B:\abs{x}\leqq1$ かつ $\abs{y}\leqq1$ より,$B$ が表す領域は下図の斜線部分(境界を含む)である。
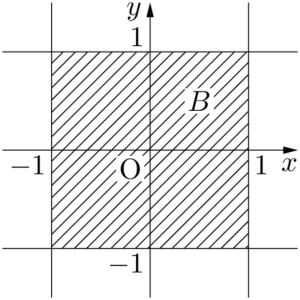
$a=1$ のときを調べる。$A:\abs{x}+\abs{y}\leqq1$ より,$A$ が表す領域は下図の斜線部分(境界を含む)となる。$B$ が表す領域と重ねて描いている。
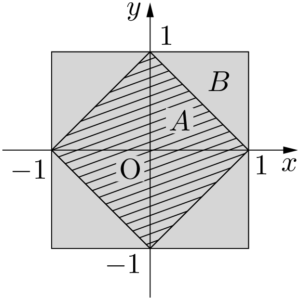
$A$ が表す領域は $B$ が表す領域に含まれるから,$A$ ならば $B$ が成り立つ。したがって,$A$ は $B$ の十分条件である。よって,選択肢は「2」である。
次に $a=2$ のときを調べる。$A:\abs{x}+\abs{y}\leqq2$ より,$A$ が表す領域は下図の斜線部分(境界を含む)となる。
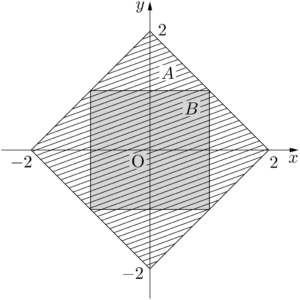
$A$ が表す領域は $B$ が表す領域を含むから,$B$ ならば $A$ が成り立つ。したがって,$A$ は $B$ の必要条件である。よって,選択肢は「1」である。
$a$ の値にかかわらず,$B$ が表す領域は変わらないから,$B$ が表す領域を図示することから始める。
$B:\abs{x}\leqq1$ かつ $\abs{y}\leqq1$ より,$B$ が表す領域は下図の斜線部分(境界を含む)である。

$a=1$ のときを調べる。$A:\abs{x}+\abs{y}\leqq1$ より,$A$ が表す領域は下図の斜線部分(境界を含む)となる。$B$ が表す領域と重ねて描いている。

$A$ が表す領域は $B$ が表す領域に含まれるから,$A$ ならば $B$ が成り立つ。したがって,$A$ は $B$ の十分条件である。よって,選択肢は「2」である。
次に $a=2$ のときを調べる。$A:\abs{x}+\abs{y}\leqq2$ より,$A$ が表す領域は下図の斜線部分(境界を含む)となる。

$A$ が表す領域は $B$ が表す領域を含むから,$B$ ならば $A$ が成り立つ。したがって,$A$ は $B$ の必要条件である。よって,選択肢は「1」である。



















