今回は,通過する3点が定められた円の方程式について説明します。
円の方程式を一般形でおくと,3文字の連立方程式を解く必要がありますが,正確に計算できるようにしましょう。
また,余裕があれば,連立方程式を解かないで済む求め方をマスターしましょう。
3点を与えたときは円は1つに定まる

ヒロ
まず,通るべき3点を与えると,その円は1つに定まることを理解しよう。
平面上に一直線上にない3点P,Q,Rを通る円$C$ を考える。円の中心をCとすると,点Cは3点P,Q,Rから距離が等しい位置にある。2点から等距離にある点の集合は,その2点を結ぶ線分の垂直二等分線であるから,線分PQの垂直二等分線と線分QRの垂直二等分線の交点が,円 $C$ の中心である。
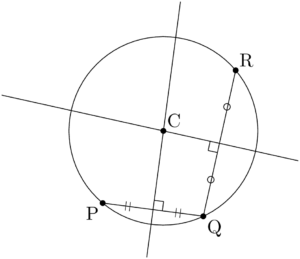
上図のように,3点P,Q,Rから円の中心Cが1つに定まる。中心Cにコンパスの針を刺して,点Pを通るように半径を調整して円を描くと,当たり前であるがその円は残りの2点Q,Rも自動的に通る。


















