3点を通る円の方程式の求め方

3点を通る円の方程式を求める方法としては,主に3つの方法がある。
- 円の中心と半径を求める。
- 円の方程式を一般形でおいて,係数を求める。
- 2点を通る円の方程式を利用する。

順番に説明するが,3番目の方法については,次の記事で扱っている。
円の中心と半径を求める

次の問題を用いて説明する。
(1) 線分OAの垂直二等分線の方程式を求めよ。
(2) 3点O,A,Bを通る円の方程式を求めよ。
OAの傾きは $\dfrac{3}{2}$ であり,中点をMとするとM$\left(1,~\dfrac{3}{2}\right)$ であるから,線分OAの垂直二等分線の方程式は
&y=-\dfrac{2}{3}(x-1)+\dfrac{3}{2} \\[4pt]
&y=-\dfrac{2}{3}x+\dfrac{13}{6}~\cdots\cdots①
\end{align*}
(2) 3点O,A,Bを通る円の方程式を求めよ。
弦の垂直二等分線が円の中心を通ることから,(1)がその誘導になっていることに気付けるようにしよう。垂直二等分線をもう1本求めれば,連立方程式を解くことでその交点,すなわち円の中心を求めることができる。線分OBの垂直二等分線と線分ABの垂直二等分線でどちらがより簡単に求められるかを考えよう。OBの垂直二等分線なら,(1)と同様に求めることができるはず。ABの垂直二等分線を求めようとすると,2点A,Bの座標に着目することになり,$y$ 座標が等しいことに気付く。つまり,線分ABの垂直二等分線は $x$ 軸に垂直な直線となるため,こちらの方が簡単に求めることができる。
ABの中点は $\left(-\dfrac{1}{2},~3\right)$ であるから,ABの垂直二等分線の方程式は $x=-\dfrac{1}{2}~\cdots\cdots②$ である。②を①に代入すると
y&=-\dfrac{2}{3}\Cdota\left(-\dfrac{1}{2}\right)+\dfrac{13}{6} \\[4pt]
&=\dfrac{15}{6}=\dfrac{5}{2}
\end{align*}
r^2&=\text{OC}^2 \\[4pt]
&=\left(-\dfrac{1}{2}\right)^2+\left(\dfrac{5}{2}\right)^2 \\[4pt]
&=\dfrac{26}{4}=\dfrac{13}{2}
\end{align*}
\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{5}{2}\right)^2=\dfrac{13}{2}
\end{align*}
円の方程式を一般形でおいて,係数を求める。

この問題を見て,点Bの座標だけが面倒な設定だなと思うだろう。

このことを深読みすると,あることを想定するが,これについては後で説明する。

とりあえず一般形でおいて円の方程式を求めよう。
求める円の方程式は
C:x^2+y^2+lx+my+n=0
\end{align*}
&4+1+2l-m+n=0 \\[4pt]
&2l-m+n=-5~\cdots\cdots①
\end{align*}
&(2\sqrt{6}-1)^2+4+(2\sqrt{6}-1)l+2m+n=0 \\[4pt]
&(2\sqrt{6}-1)l+2m+n=-29+4\sqrt{6}~\cdots\cdots②
\end{align*}
&16+49-4l+7m+n=0 \\[4pt]
&-4l+7m+n=-65~\cdots\cdots③
\end{align*}
$①-②$ より
&(3-2\sqrt{6})l-3m=24-4\sqrt{6}~\cdots\cdots④
\end{align*}
&6l-8m=60 \\[4pt]
&3l-4m=30~\cdots\cdots⑤
\end{align*}
&(3-8\sqrt{6})l=6-16\sqrt{6} \\[4pt]
&l=2
\end{align*}
&6-4m=30 \\[4pt]
&m=-6
\end{align*}
&4+6+n=5 \\[4pt]
&n=-5
\end{align*}
x^2+y^2+2x-6y-5=0
\end{align*}

この問題では,点Bの座標だけに無理数があり,それが原因で面倒な計算になる。

受験生を苦しめるためだけに,このような面倒な設定がされているのだろうか?という疑問を持つ人もいるだろう。

そのような疑問をもった場合は「もしかすると,簡単になるように点Bを定めてくれているのではないか?」と思うだろう。

つまり「2点A,Cを直径の両端として決めた後,その円周上の点としてBをとったのではないか?点Bの $y$ 座標を2という整数に決めたが,結果として $x$ 座標だけが無理数になってしまった。」と考えてしまう。

この座標の設定の不自然さから,次のような確認をした。
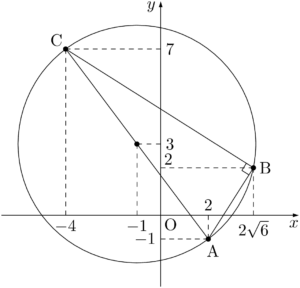
3点A$(2,~-1)$,B$(2\sqrt{6}-1,~2)$,C$(-4,~7)$ を通る円の方程式を求めよ。
ABの傾き $m$ を計算すると,$\dfrac{3}{2\sqrt{6}-3}$ であり,BCの傾き $n$ を計算すると,$\dfrac{-5}{2\sqrt{6}+3}$ である。ABとBCの傾きの積を計算すると
mn&=\dfrac{3}{2\sqrt{6}-3}\Cdota\dfrac{-5}{2\sqrt{6}+3} \\[4pt]
&=\dfrac{-15}{24-9}=-1
\end{align*}
これより,3点A,B,Cを通る円は線分ACを直径とする円となる。ACの中点をMとすると,M$(-1,~3)$ となる。
また,ACの長さの半分が半径 $r$ であるから
r^2&=\dfrac{\text{AC}^2}{4} \\[4pt]
&=\dfrac{6^2+(-8)^2}{4} \\[4pt]
&=\dfrac{36+64}{4}=25
\end{align*}
(x+1)^2+(y-3)^2=25
\end{align*}

上のように傾きの積でなく,三平方の定理が成り立つかどうかを確認する人もいるだろう。

その場合は次のようになる。
A$(2,~-1)$,B$(2\sqrt{6}-1,~2)$,C$(-4,~7)$ より
&\text{AB}^2=(2\sqrt{6}-3)^2+3^2=42-12\sqrt{6} \\[4pt]
&\text{BC}^2=(2\sqrt{6}+3)^2+(-5)^2=58+12\sqrt{6} \\[4pt]
&\text{CA}^2=6^2+(-8)^2=100
\end{align*}
\text{AB}^2+\text{BC}^2=\text{CA}^2
\end{align*}

好みの問題であるとは思うが,個人的には,傾きの積が $-1$ になることを確認する方が楽な気がする。

今回は与えられている座標の不自然さから,傾きの積を確認して,結果として上手くいった。

しかし,問題によっては,座標設定が面倒になっているだけのものもあるので,いつもこのように上手くいくとは限らない。



















