Contents
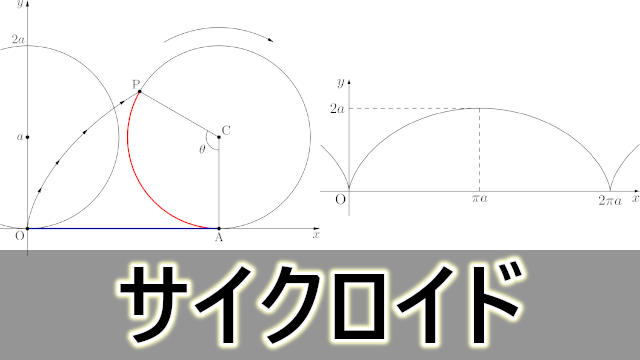
サイクロイド曲線の長さ

ヒロ
サイクロイド曲線の長さを求めよう。
$\dfrac{dx}{d\theta},~\dfrac{dy}{d\theta}$ は
よって
\begin{align*}
\begin{cases}
\dfrac{dx}{d\theta}=a(1-\cos\theta) \\[4pt]
\dfrac{dy}{d\theta}=a\sin\theta
\end{cases}
\end{align*}
となるから\begin{cases}
\dfrac{dx}{d\theta}=a(1-\cos\theta) \\[4pt]
\dfrac{dy}{d\theta}=a\sin\theta
\end{cases}
\end{align*}
\begin{align*}
&\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2} \\[4pt]
&=\sqrt{a^2(1-\cos\theta)^2+a^2\sin^2\theta} \\[4pt]
&=\sqrt{2a^2(1-\cos\theta)} \\[4pt]
&=\sqrt{4a^2\sin^2\dfrac{\theta}{2}} \\[4pt]
&=2a\abs{\sin\dfrac{\theta}{2}}
\end{align*}
$0\leqq \theta\leqq\pi$ のとき,$0\leqq\dfrac{\theta}{2}\leqq\dfrac{\pi}{2}$ であるから,$\sin\dfrac{\theta}{2}\geqq0$&\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2} \\[4pt]
&=\sqrt{a^2(1-\cos\theta)^2+a^2\sin^2\theta} \\[4pt]
&=\sqrt{2a^2(1-\cos\theta)} \\[4pt]
&=\sqrt{4a^2\sin^2\dfrac{\theta}{2}} \\[4pt]
&=2a\abs{\sin\dfrac{\theta}{2}}
\end{align*}
よって
\begin{align*}
\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}=2a\sin\dfrac{\theta}{2}
\end{align*}
したがって,求めるサイクロイド曲線の長さを $L$ とすると\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}=2a\sin\dfrac{\theta}{2}
\end{align*}
\begin{align*}
L&=\dint{0}{2\pi}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\;d\theta \\[4pt]
&=\dint{0}{2\pi}2a\sin\dfrac{\theta}{2}\;d\theta \\[4pt]
&=\tint{-4a\cos\dfrac{\theta}{2}}{0}{2\pi} \\[4pt]
&=8a
\end{align*}
L&=\dint{0}{2\pi}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\;d\theta \\[4pt]
&=\dint{0}{2\pi}2a\sin\dfrac{\theta}{2}\;d\theta \\[4pt]
&=\tint{-4a\cos\dfrac{\theta}{2}}{0}{2\pi} \\[4pt]
&=8a
\end{align*}
サイクロイド曲線の回転体の体積

ヒロ
サイクロイド曲線で囲まれる部分を $x$ 軸のまわりに1回転してできる立体の体積 $V$ を求めよう。
$0\leqq x\leqq2\pi a$ の部分を $x$ 軸のまわりに1回転してできる立体の体積を求める。
\begin{align*}
V&=\dint{0}{2\pi a}\pi y^2\;dx \\[4pt]
&=\dint{0}{2\pi}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=\pi\dint{0}{2\pi}a^2(1-\cos\theta)^2\Cdota a(1-\cos\theta)\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}(1-3\cos\theta+3\cos^2\theta-\cos^3\theta)\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}\left\{1-3\cos\theta+\dfrac32(1+\cos2\theta)-(1-\sin^2\theta)\cos\theta\right\}\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}\left(\dfrac{5}{2}-4\cos\theta+\dfrac{3}{2}\cos2\theta+\sin^2\theta\cos\theta\right)\;d\theta \\[4pt]
&=\pi a^3\Tint{\dfrac{5}{2}\theta-4\sin\theta+\dfrac{3}{4}\sin2\theta+\dfrac{1}{3}\sin^3\theta}{0}{2\pi} \\[4pt]
&=5\pi^2a^3
\end{align*}
V&=\dint{0}{2\pi a}\pi y^2\;dx \\[4pt]
&=\dint{0}{2\pi}\pi y^2\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=\pi\dint{0}{2\pi}a^2(1-\cos\theta)^2\Cdota a(1-\cos\theta)\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}(1-3\cos\theta+3\cos^2\theta-\cos^3\theta)\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}\left\{1-3\cos\theta+\dfrac32(1+\cos2\theta)-(1-\sin^2\theta)\cos\theta\right\}\;d\theta \\[4pt]
&=\pi a^3\dint{0}{2\pi}\left(\dfrac{5}{2}-4\cos\theta+\dfrac{3}{2}\cos2\theta+\sin^2\theta\cos\theta\right)\;d\theta \\[4pt]
&=\pi a^3\Tint{\dfrac{5}{2}\theta-4\sin\theta+\dfrac{3}{4}\sin2\theta+\dfrac{1}{3}\sin^3\theta}{0}{2\pi} \\[4pt]
&=5\pi^2a^3
\end{align*}
サイクロイド曲線の性質についてのまとめ

ヒロ
サイクロイド曲線の性質についてまとめると次のようになる。
サイクロイド曲線
- グラフの概形
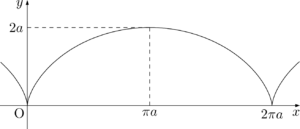
- 媒介変数表示\begin{align*}
x=a(\theta-\sin\theta),~~y=a(1-\cos\theta)
\end{align*} - 面積\begin{align*}
S=3\pi a^2
\end{align*} - 曲線の長さ\begin{align*}
L=8a
\end{align*} - 回転体の体積\begin{align*}
V=5\pi^2a^3
\end{align*}