Contents
サイクロイド曲線の描画

ヒロ
媒介変数表示された関数のグラフを描こう。

ヒロ
ここでは $0\leqq\theta\leqq2\pi$ の範囲の増減表を書いておく。
$\begin{cases}
x=a(\theta-\sin\theta) \\[4pt]
y=a(1-\cos\theta)
\end{cases}$より,
x=a(\theta-\sin\theta) \\[4pt]
y=a(1-\cos\theta)
\end{cases}$より,
\begin{align*}
\begin{cases}
\dfrac{dx}{d\theta}=a(1-\cos\theta) \\[4pt]
\dfrac{dy}{d\theta}=a\sin\theta
\end{cases}
\end{align*}
$\dfrac{dx}{d\theta}=0$ とすると,\begin{cases}
\dfrac{dx}{d\theta}=a(1-\cos\theta) \\[4pt]
\dfrac{dy}{d\theta}=a\sin\theta
\end{cases}
\end{align*}
\begin{align*}
&\cos\theta=1 \\
&\theta=0,~2\pi
\end{align*}
$\dfrac{dy}{d\theta}=0$ とすると,&\cos\theta=1 \\
&\theta=0,~2\pi
\end{align*}
\begin{align*}
&\sin\theta=0 \\
&\theta=0,~\pi,~2\pi
\end{align*}
よって,増減は次のようになる。&\sin\theta=0 \\
&\theta=0,~\pi,~2\pi
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
\theta & 0 & \cdots & \pi & \cdots & 2\pi \\\hline
\dfrac{dx}{d\theta} & 0 & + & + & + & 0 \\\hline
\dfrac{dy}{d\theta} & 0 & + & 0 & – & 0 \\\hline
(x,~y) & (0,~0) & \nearrow & (\pi a,~2a) & \searrow & (2\pi a,~0) \\\hline
\end{array}
\end{align*}
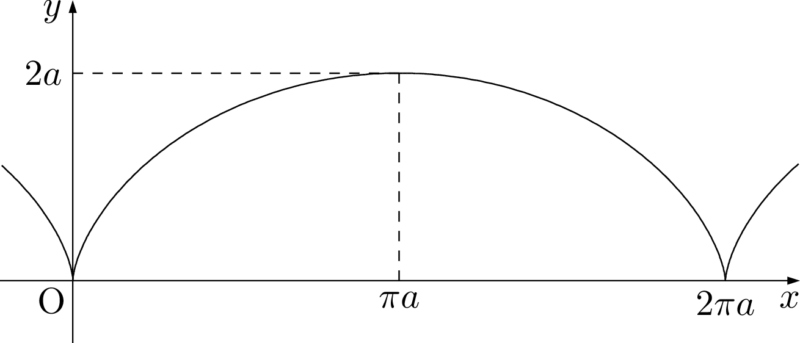
よって,サイクロイドのグラフは図のようになる。\begin{array}{|c||c|c|c|c|c|}\hline
\theta & 0 & \cdots & \pi & \cdots & 2\pi \\\hline
\dfrac{dx}{d\theta} & 0 & + & + & + & 0 \\\hline
\dfrac{dy}{d\theta} & 0 & + & 0 & – & 0 \\\hline
(x,~y) & (0,~0) & \nearrow & (\pi a,~2a) & \searrow & (2\pi a,~0) \\\hline
\end{array}
\end{align*}

サイクロイド曲線で囲まれる部分の面積

ヒロ
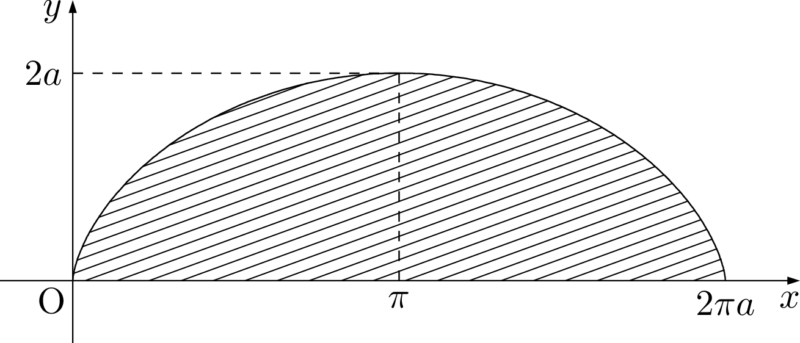
サイクロイド曲線で囲まれる部分の面積 $S$ を求めよう。
斜線部分の面積 $S$ を求める。

\begin{align*}
S&=\dint{0}{2\pi a}y\;dx \\[4pt]
&=\dint{0}{2\pi}y\Cdota\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}(1-\cos\theta)^2\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}(1-2\cos\theta+\cos^2\!\theta)\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}\left(1-2\cos\theta+\dfrac{1+\cos2\theta}{2}\right)\;d\theta \\[4pt]
&=a^2\Tint{\dfrac{3}{2}\theta-2\sin\theta+\dfrac{1}{4}\sin2\theta}{0}{2\pi} \\[4pt]
&=3\pi a^2
\end{align*}
S&=\dint{0}{2\pi a}y\;dx \\[4pt]
&=\dint{0}{2\pi}y\Cdota\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}(1-\cos\theta)^2\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}(1-2\cos\theta+\cos^2\!\theta)\;d\theta \\[4pt]
&=a^2\dint{0}{2\pi}\left(1-2\cos\theta+\dfrac{1+\cos2\theta}{2}\right)\;d\theta \\[4pt]
&=a^2\Tint{\dfrac{3}{2}\theta-2\sin\theta+\dfrac{1}{4}\sin2\theta}{0}{2\pi} \\[4pt]
&=3\pi a^2
\end{align*}