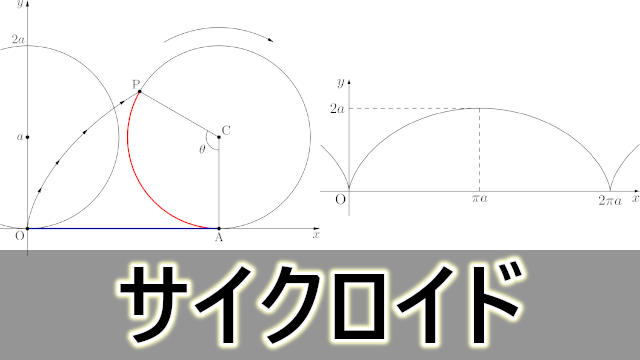
定直線に沿って円が滑らずに回転するときの円周上の定点の軌跡をサイクロイドといいます。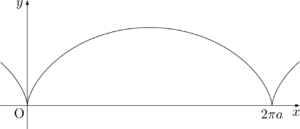
サイクロイド曲線の媒介変数表示,曲線の描画,面積,曲線の長さ,回転体の体積について知っておきましょう。
Contents
サイクロイド曲線の媒介変数表示

ヒロ
サイクロイド上の点 $\mathrm{P}(x,~y)$ の媒介変数表示を導こう。
点 $(0,~a)$ を中心とする半径 $a$ の円 $C$ が $x$ 軸上を滑らずに転がり,円 $C$ の中心が点Cまできたとき,原点の位置にあった点が移動した点をPとし,$\kaku{ACP}=\theta$ とする。
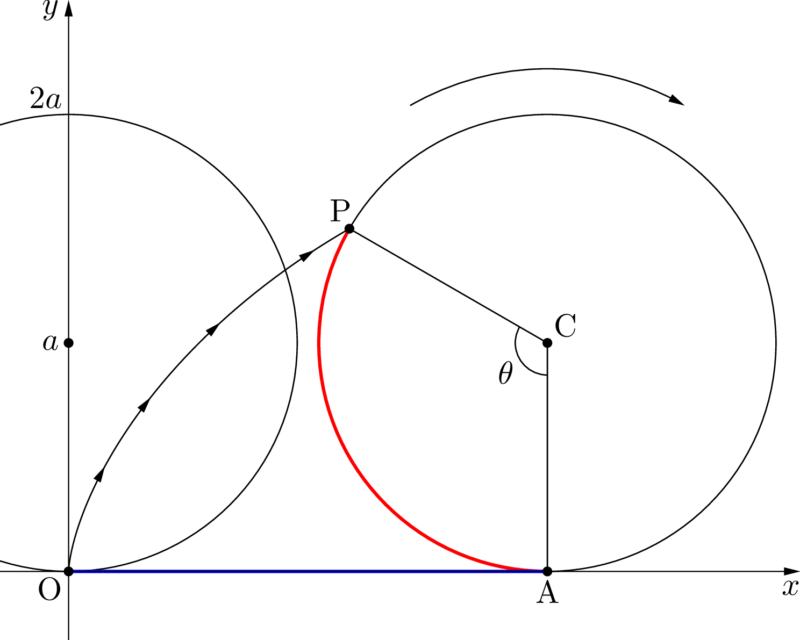
このとき,線分OAの長さと弧APの長さが等しくなるから
点Cを中心に $\Vec{CA}$ を $-\theta$ だけ回転したものが $\Vec{CP}$ であるから,点Pを表す複素数を $z$ とすると,

このとき,線分OAの長さと弧APの長さが等しくなるから
\begin{align*}
\mathrm{OA}=\ko{\mathrm{AP}}=a\theta
\end{align*}
複素数平面上で考えると,点A, Cを表す複素数はそれぞれ $a\theta$, $a\theta+ia$ となる。\mathrm{OA}=\ko{\mathrm{AP}}=a\theta
\end{align*}
点Cを中心に $\Vec{CA}$ を $-\theta$ だけ回転したものが $\Vec{CP}$ であるから,点Pを表す複素数を $z$ とすると,
\begin{align*}
z&=\bigl(\cos(-\theta)+i\sin(-\theta)\bigr)(-ia)+a\theta+ia \\[4pt]
&=a(\theta-\sin\theta)+ia(1-\cos\theta)
\end{align*}
$z=x+iy$ よりz&=\bigl(\cos(-\theta)+i\sin(-\theta)\bigr)(-ia)+a\theta+ia \\[4pt]
&=a(\theta-\sin\theta)+ia(1-\cos\theta)
\end{align*}
\begin{align*}
\begin{cases}
x=a(\theta-\sin\theta)\\[4pt]
y=a(1-\cos\theta)
\end{cases}
\end{align*}
\begin{cases}
x=a(\theta-\sin\theta)\\[4pt]
y=a(1-\cos\theta)
\end{cases}
\end{align*}